Carlos N. Rautenberg

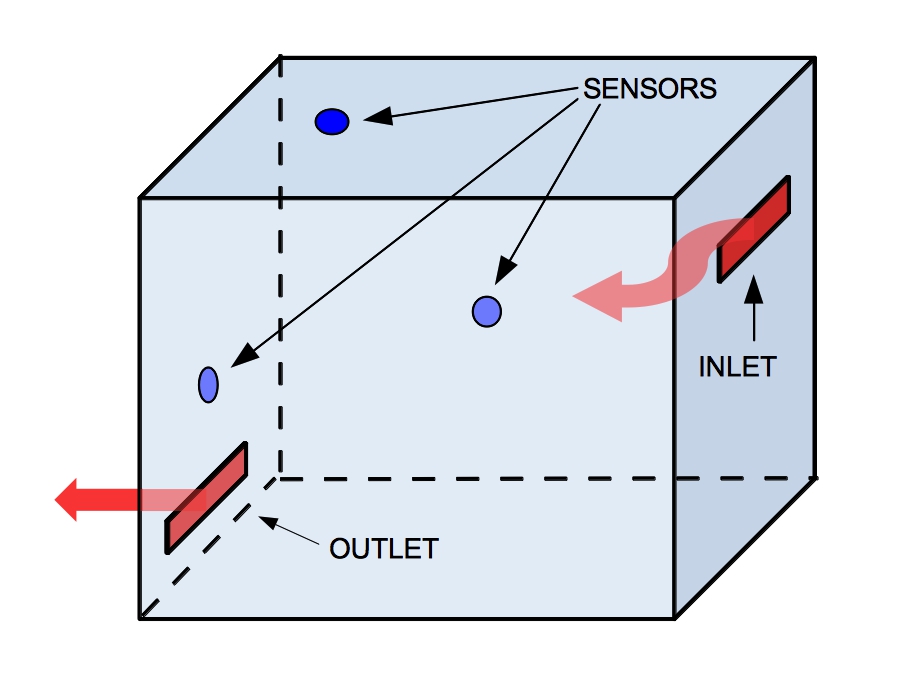
The optimal placement of sensors (such as thermostats) is usually a complex multiscale problem where multiple nonlinear processes are coupled. Here we assume $\Omega$ is a room or building where sensors are placed and a ventilation system is in place with an outlet and an inlet; see Fig. 1. The temperature of the room is determined by $u$ such $u:\Omega\to\mathbb{R}^n$ , and it is advected by a the velocity profile of the air $\vec{v}:\Omega\to\mathbb{R}^{n\times n}$.

Fig.1-Room sample.

The convection-diffusion process is perturbed by an stochastic (Wiener) process $\eta$. We measure $u$ with a sensor in location $x$ by a weighted average within an effective range and obtain an output $h_x$ which is also perturbed by an stochastic process $\nu$. The system satisfied by this variables is given by they are \begin{align*} u'&=\alpha\Delta u+v\cdot\nabla u+ \eta;\\ h_x&=C(x)u+\nu; \end{align*} where the sensor action is described by \begin{align*} C(x)w=\int_{\Omega}K(y-x)w(y) dy, \end{align*} where $K$ is some function obtained from properties of the sensor. A good criteria for good a sensor is placed is obtained by trying to minimize the expected value of $|u-\tilde{u}_x|^2_{L^2(\Omega)}$ where $\tilde{u}_x$ is the output of the Kalman Filter.

For simple problems, where $\vec{v}$ is considered constant, isosurfaces for \begin{align*} x\mapsto J(x):=\int_0^1 \mathbb{E}\|u-\tilde{u}_x\|_{L^2}^2 dt \end{align*} seem to be associated to a convex problem (see Figure 2). In cases where the kernel function $K$ is non-smooth and/or $\vec{v}$ is not constant and it is the solution to Navier-Stokes on the domain of interest (+ appropriate boundary conditions), $x\mapsto \int_0^1 \mathbb{E}|u-\tilde{u}_x|_{L^2}^2 dt$ does not longer seem to come from a convex problem as shown in Figure 3.