Topology, Algebraic Geometry, and Dynamics Seminar (TADS)

 

TADS is a venue for presentation/discussion concerning topology, algebraic geometry, or dynamics (broadly understood).

Attendance is open, and those interested in giving a talk should e-mail title/abstract to any committee member (dcarched, or alukyane at gmu.edu). Talks are 50-90 minutes, and will, for the time being, take place on Zoom:

ZOOM LINK.

Speakers are given the opportunity to have their presentations recorded: YouTube.

TADS Committee: David Carchedi (chair), Anton Lukyanenko

Fall 2020: Fridays 1:30-3:00 PM

• Friday, December 4, 2020
  Notre Dame, Pavel Mnev
  


Chern-Simons theory on cylinders and generalized Hamilton-Jacobi actions


We study the perturbative path integral of Chern-Simons theory on a cylinder [0,1]x Sigma with a holomorphic polarization on the boundaries, in the context of Batalin-Vilkovisky quantization (or rather its variant compatible with cutting-gluing, the “BV-BFV quantization”). We find that, in the case of non-abelian 3D Chern-Simons, the fiber BV integral for the system produces the gauged WZW model on Sigma. Classically, the result corresponds to computing a “generalized Hamilton-Jacobi action” for Chern-Simons theory on a cylinder — a generating function (in an appropriate sense) for the evolution relation induced on the boundary conditions by the equations of motion. A similar setup applied to 7D abelian Chern-Simons on a cylinder [0,1] x Sigma, with Sigma a Calabi-Yau of (real) dimension 6, with a linear polarization on one side and a nonlinear (Hitchin) polarization on the other side, is related to the Kodaira-Spencer (a.k.a. BCOV) theory. In the talk, I will introduce the concept of generalized Hamilton-Jacobi functions in the example of classical mechanics with constraints described by an equivariant moment map and proceed to discuss the examples above. This is a report on a joint work with Alberto S. Cattaneo and Konstantin Wernli.


• Friday, November 20, 2020
  Cary Malkiewich, Binghamton University
  


The higher characteristic polynomial


Abstract: In this talk I will discuss various lifts of the characteristic polynomial to the setting of algebraic K-theory, and describe the relationship to trace methods and to topological fixed-point theory and dynamics.


• November 13, 2020
  Theo Johnson-Freyd, Dalhousie University, Perimeter Institute
  


Holomorphic SCFTs of small index


Abstract: I will explain how some questions in theoretical physics and algebraic topology led to a curious result about error-correcting ternary codes. No knowledge of the terms in the title or abstract will be assumed. Based on joint work with Davide Gaiotto.


Spring 2020

• February 28, 2020
  Akhil Mathew, University of Chicago
  


A gentle approach to crystalline cohomology


Given a smooth algebraic variety X over C, a classical result of Grothendieck shows that one can recover the singular cohomology of X (with complex coefficients) using only algebraic differential forms. In characteristic p, the analogous construction also works but is less satisfactory: it produces only p-torsion cohomology groups. The de Rham-Witt complex (or crystalline cohomology) provides an integral lift, and yields one of the basic cohomology theories for varieties in characteristic p. In this talk, I will explain a new approach to the de Rham-Witt complex based only on elementary homological algebra. Joint work with Bhargav Bhatt and Jacob Lurie.


• February 21, 2020
  Owen Gwilliam, UMass Amhrest
  


Factorization algebras in topology and physics


Factorization homology arises in algebraic topology as a nonlinear generalization of homology theory a la Eilenberg-Steenrod. The first part of my talk will focus on developing the notions of factorization algebra and factorization homology, as articulated by Ayala-Francis and Lurie. In the second part I will discuss how factorization algebras arise naturally in classical and quantum field theory. The goal is to explain recent joint work with Eugene Rabinovich and Brian Williams about field theory on manifolds with boundary, which offers a useful perspective on Kontsevich's deformation quantization of Poisson manifolds as well as the relationship of loop groups to quantum groups via perturbative Chern-Simons theory.


• February 7, 2020
  Suhyoung Choi, KAIST
  


Title: Closed affine manifolds with partially hyperbolic linear holonomy


We give some introduction to the field of complete affine n-manifolds, ,i.e., quotients of the affine n-space by properly discontinuous actions of affine transformation groups. We will try to show that closed manifolds of negative curvature do not admit complete special affine structures whose linear parts are partially hyperbolic in the dynamical sense. We can drop the negative curvature condition. We present our attempt here. (Partially a joint work with Kapovich.)


Fall 2019

• December 6, 2019
  Grace Work, Girls' Angle and M.I.T.
  


Title: Discretely shrinking targets in moduli space*
*This talk will begin at 10:30a.m.


Abstract: Consider a nested family of target sets shrinking at a specified rate and a given flow, we want to understand the set of points whose orbits hit these targets infinitely often under the flow. One way to examine this set is to determine under what conditions this set has full measure. This question is closely related to the Borel-Cantelli Lemma and also gives rise to logarithm laws. In joint work with Spencer Dowdall we examine this particular question for Teichmuller flow on the moduli space of unit-area quadratic differentials.


• November 22, 2019
  Elizabeth Milicevic, Haverford College

  
  The Peterson Isomorphism: Moduli of Curves and Alcove Walks
  In this talk, I will explain the combinatorial tool of folded alcove walks, in addition to surveying a wide range of applications in combinatorics, representation theory, and algebraic geometry. As a concrete example, I will describe a labeling of the points of the moduli space of genus zero curves in the complete complex flag variety using the combinatorial machinery of alcove walks. Following Peterson, this geometric labeling partially explains the "quantum equals affine" phenomenon which relates the quantum cohomology of this flag variety to the homology of the affine Grassmannian. This is joint work with Arun Ram.



• November 15, 2019
  Julianna Tymoczko, Smith College

  
  An introduction to generalized splines
  Splines are a fundamental tool in applied mathematics and analysis, classically described as piecewise polynomials on a combinatorial decomposition of a geometric object (a triangulation of a region in the plane, say) that agree up to a specified differentiability on faces of codimension one. Generalized splines extend this idea algebraically and combinatorially: instead of certain classes of geometric objects, we start with an arbitrary combinatorial graph; instead of labeling faces with polynomials, we label vertices with elements of an arbitrary ring; and instead of applying degree and differentiability constraints, we require that the difference between ring elements associated to adjacent vertices is in a fixed ideal labeling the edge. Billera showed that these two characterizations coincide in most cases of real-world interest. In this talk, we describe some of the differences between generalized splines and classical splines, and some of the implications of results about generalized splines for classical splines.



• November 1, 2019
  Brent Gorbutt, George Mason University

  
  Strings of beads and the equivariant cohomology or Peterson varieties*
  *This talk will be at 11:30am
  
  Understanding the product structure of cohomology rings of Grassmann manifolds and flag manifolds is an area of classical interest. For certain special bases of cohomology rings of these spaces, products of basis elements are known to be positive and integral linear combinations of other basis elements for appropriate notions of ``positive'' and ``integral.''. In this talk I'll present a positive and integral formula for special basis elements of the equivariant cohomology of the Peterson variety, which is a subvariety of the complete flag manifold. I'll also discuss a previously unknown combinatorial identity that was discovered and used in the proof of the product formula in the equivariant cohomology of the Peterson variety.



• October 18, 2019
  Changlong Zhong, SUNY Albany

  
  K-theory stable basis of Springer resolutions*
  *This talk will be at 10:30am
  
  In this talk I will recall the definition of K-theory stable basis of Springer resolutions, defined by Maulik-Okounkov. It plays important role in calculation of quantum K-theory, and has close relationship with the motivic Chern classes of Schubert varieties from algebraic geometry. I will also mention its relation with affine Hecke algebra action, restriction formula, and wall-crossing matrices. This is joint work with Changjian Su and Gufang Zhao.



• October 4, 2019
  Anders Buch, Rutgers University

  
  Positivity determines quantum cohomology
  I will show that the small quantum cohomology ring of a Grassmannian is, up to rescaling the deformation parameter q, the only graded q-deformation of the singular cohomology ring with non-negative Schubert structure constants. This implies that the (three point, genus zero) Gromov-Witten invariants are uniquely determined by Witten's presentation of the quantum ring and the fact that they are non-negative. A similar statement appears to be true for any flag variety of simply laced Lie type. For the variety of complete flags, this statement is equivalent to Fomin, Gelfand, and Postnikov's conjecture that the quantum Schubert polynomials are uniquely determined by positivity properties. The proof for Grassmannians answers a question of Fulton. This is joint work with Chengxi Wang.



• September 20, 2019
  Leonardo Mihalcea, Virginia Tech

  
  Cotangent Schubert Calculus
  Modern Schubert Calculus studies various intersection rings associated to flag manifolds. All these rings have several common features: they all have a distinguished Schubert basis; the Schubert structure constants count points; the Schubert classes can be defined by equivariant localization. A question with roots in representation theory and microlocal analysis is whether there are good analogues of Schubert classes to study intersection rings of the cotangent bundle of a flag manifold. One answer is given in terms of the characteristic classes of singular subvarieties in the flag manifold, such as the Chern-Schwartz-MacPherson classes. For flag manifolds, these classes are equivalent to the stable envelopes on the cotangent bundle, defined recently by Maulik and Okounkov. I will explain these ideas, and draw parallels with the Schubert Calculus situation. For instance, instead of counting points in three Schubert cycles, in the cotangent situation one takes the Euler characteristic of the intersection of three Schubert cells.



• September 6, 2019
  Andrei Rapinchuk, University of Virginia

  
  Groups with good reduction
  The techniques involving reduction are common in number theory and arithmetic geometry. In particular, elliptic curves and general abelian varieties with good reduction have been the subject of a very intensive investigation over the years. The purpose of this talk is to report on the recent work that focuses on the analysis of good reduction in the context of linear algebraic groups. More precisely, let $G$ be a reductive algebraic group over a field $K$, and assume that $K$ is equipped with a ``natural" set $V$ of discrete valuations. We are interested in the $K$-forms of $G$ that have good reduction at all $v$ in $V$. In the case $K$ is the fraction field of a Dedekind domain, a similar question was considered by G.~Harder; the case $K = \mathbb{Q}$ and $V$ is the set of all $p$-adic places was treated in detail by B.H.~Gross and B.~Conrad. I will discuss the emerging results in the higher-dimensional situation where $K$ is the function field $k(C)$ of a smooth geometrically integral curve $C$ over a number field $k$, or even an arbitrary finitely generated field. I will also indicate connections with other questions involving the genus of $G$ (i.e., the set of isomorphism classes of $K$-forms of $G$ having the same isomorphism classes of maximal tori as $G$), the Hasse principle, weakly commensurable Zariski-dense subgroups, etc. (Joint work with V. Chernousov and I. Rapinchuk.)
  




Spring 2019

• April 26, 2019 Polygon Spaces
  Jack Love, George Mason University
  

• April 19, 2019 Special nilpotents and Higher Teichmüller spaces
  Brian Collier, University of Maryland, College Park
  

  

• April 5, 2019 Expanding Thurston maps and visual spheres
  Annina Iseli, University of California, Los Angeles
  

  

• March 22, 2019 Capturing invariance in flows and combinatorial vector fields
  Tom Wanner, George Mason University
  

• March 8, 2019 Singularities of commutative rings via test ideals
  Rebecca R.G., George Mason University
  

  

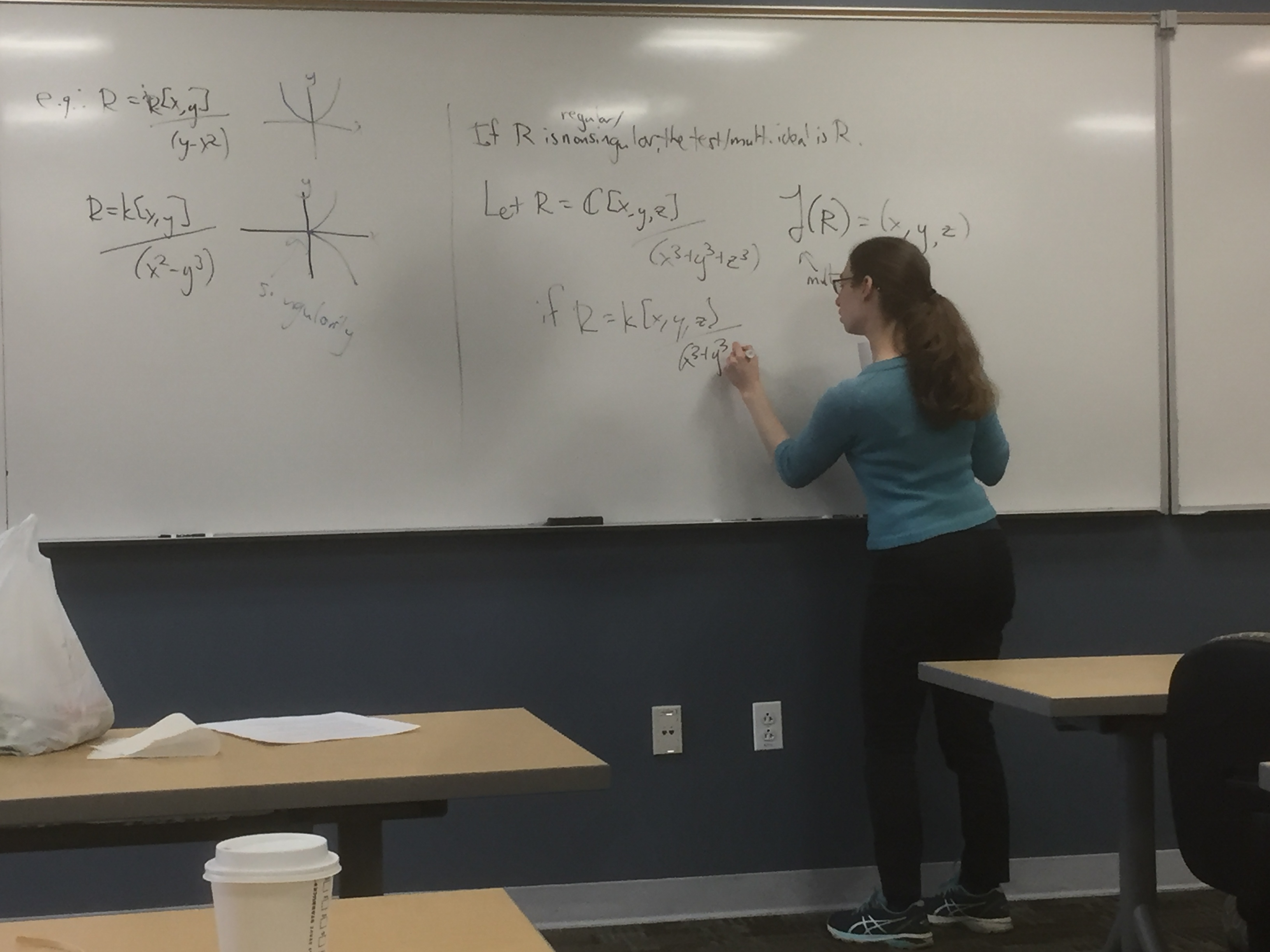
• February 22, 2019 Dynamics and the Clebsch diagonal cubic surface
  William Goldman, University of Maryland, College Park
  

  

• February 8, 2019 How self-driving robots find delivery paths, and how this leads to sub-Riemannian geometry
  Anton Lukyanenko, George Mason University
  

  

• January 25, 2019 Explicit modular forms via the homotopy groups of spheres.
  Donald Larson, Catholic University of America
  

  

Fall 2018

• November 30, 2018 Convex hulls of quasicircles in hyperbolic and anti-de Sitter space
  Sara Maloni, University of Virginia
  

  

• November 16, 2018 Battle Hymn of Discreteness
  Caleb Ashley, University of Michigan
  

  

• November 2, 2018 On some (equivariant) combinatorics related to flag manifolds
  Rebecca Goldin, GMU
  

  

• October 26, 2018 Quasi-isometries of the Baumslag-Gersten group
  Tullia Dymarz, University of Wisconsin–Madison
  

  

• September 28, 2018 Toric Vector Bundles and Piecewise Linear Maps
  Christopher Manon, University of Kentucky
  

  

• September 14, 2018 Ergodicity of Iwasawa continued fractions via markable hyperbolic geodesics
  Anton Lukyanenko, GMU
  

  

Spring 2018

• April 27, 2018 Morse theory and a stack of broken lines
  Hiro Lee Tanaka, Harvard University
  

  

• April 6, 2018 Topological realization of varieties over Spec C((t)) via log geometry
  Mattia Talpo, Simon Fraser University
  

  

• April 6, 2018 Connecting Outreach and Continued Fraction Expansions Through Tessellations
  Claire Merriman, UIUC
  Special Time: 4:40-5:30pm
  

  

• March 30, 2018 Representation stability, homological stability, and commuting matrices
  Daniel Ramras, Indiana University–Purdue University Indianapolis
  

  

• March 2, 2018 Hilbert Schemes and the Motivic Sphere Spectrum
  Elden Elmanto, Northwestern University
  

  

• February 23, 2018 Homotopy types of moduli spaces of foliations
  David Carchedi, GMU
  

  

• February 16, 2018 Some results on affine Deligne-Lusztig varieties
  Xuhua He, UMCP
  

  

• February 9, 2018 How to do Multivariable Calculus on Graphs
  Tyrus Berry, GMU
  

  

• January 23, 2018 Poisson Structure on Compactification of Moduli Space of Representations
  Sean Lawton, GMU
  

  

Fall 2017

• November 17, 2017 Lipschitz maps from PI spaces to Carnot groups
  Kyle Kinneberg
  

  

• October 20, 2017 Dirichlet domains in different geometries
  Todd Drumm, Howard University
  

  

• October 13, 2017 Homotopy types as a foundation for mathematics
  Emily Riehl, JHU
  

  

• October 6, 2017 Counting matrices with forced zero entries
  Joel Lewis, George Washington University
  

  

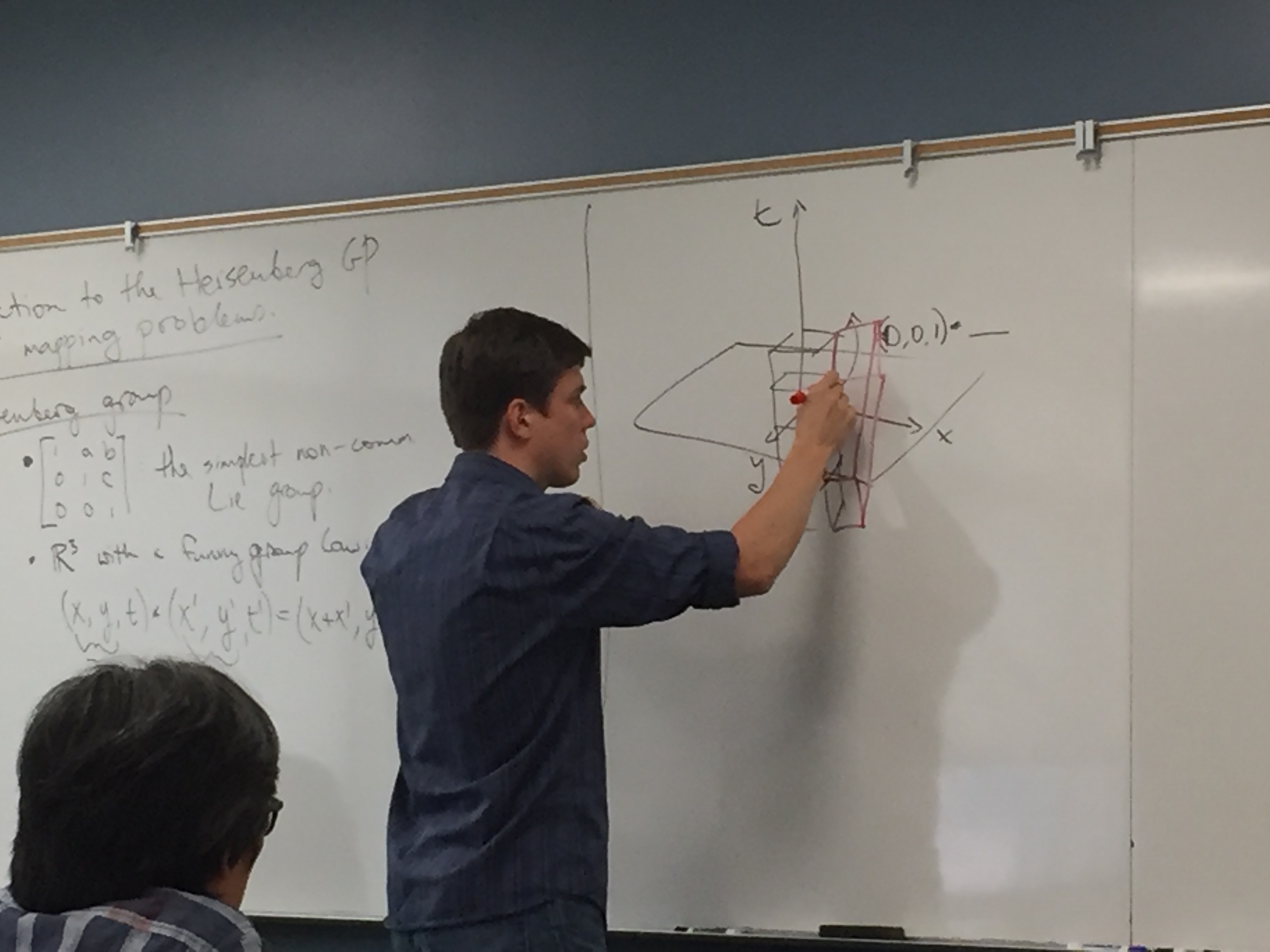
• September 22, 2017 An invitation to the Heisenberg group and its deformations
  Anton Lukyanenko, GMU
  

  

• September 15, 2017 Free products and regularity of group actions
  Thomas Koberda, UVA
  

  

• September 8, 2017 Can rotation numbers be computed from a quasiperiodic trajectory?
  Evelyn Sander, GMU
  

  

Spring 2017

• May 5, 2017 Hyperbolic localization and nearby cycles
  Tom Haines, UMCP
  

  

• April 14, 2017 The Erdos-Szekeres Problem
  Valeriu Soltan, GMU
  

  

• April 7, 2017 Quotient of surface groups and homology of finite covers via Topological Quantum Field Theories
  Ramanujan Santharoubane, University of Virginia
  

  

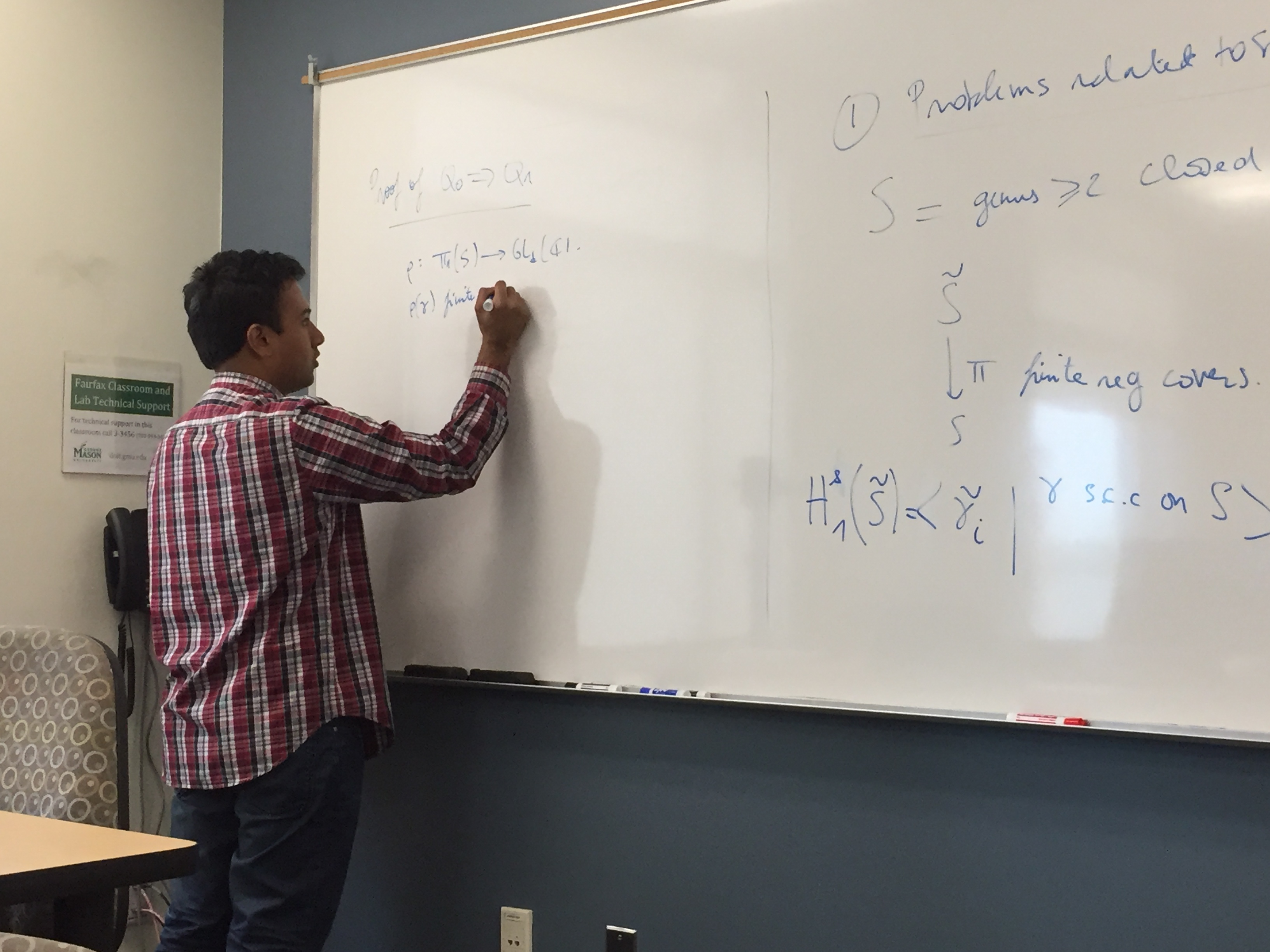
• March 24, 2017 Invertible Orbifolds over Finite Fields
  Marco Aldi, Virginia Commonwealth University
  

  

• March 10, 2017 Accessing Geometry via Function Spaces
  Tyrus Berry, GMU
  

  

• March 3, 2017 Manifolds, Schemes, Deligne-Mumford stacks, and Orbifolds: Why they’re all topoi.
  David Carchedi, GMU
  

  

• February 17, 2017 Tropical geometry of complexity 1 T -varieties
  Chris Manon, GMU
  

  

• February 10, 2017 Families of Unitary Representations and Kazhdan’s Property (T)
  Dan Ramras, IUPUI
  

  

• February 3, 2017 Compactification of Character Varieties
  Sean Lawton, GMU
  

• January 27, 2017 An introduction to 2−Segal spaces
  Julie Bergner, UVA
  

  

Fall 2016

• December 15, 2016 Tropicalization of Configurations of Flags
  Ian Le, Perimeter Institute for Theoretical Physics
  Special Date/Location: 12/15/16, Fishbowl (4th floor of Exploratory Hall)
  

  

• December 9, 2016 Operads with homological stability
  Sarah Yeakel, University of Maryland
  

  

• December 2, 2016 SO(p, q)-surface group representations
  Brian Collier, University of Maryland
  

  

• October 28, 2016 Parabolic Higgs Bundles & Generalized Parabolic Higgs Bundles
  Marina Logares, Oxford
  

  

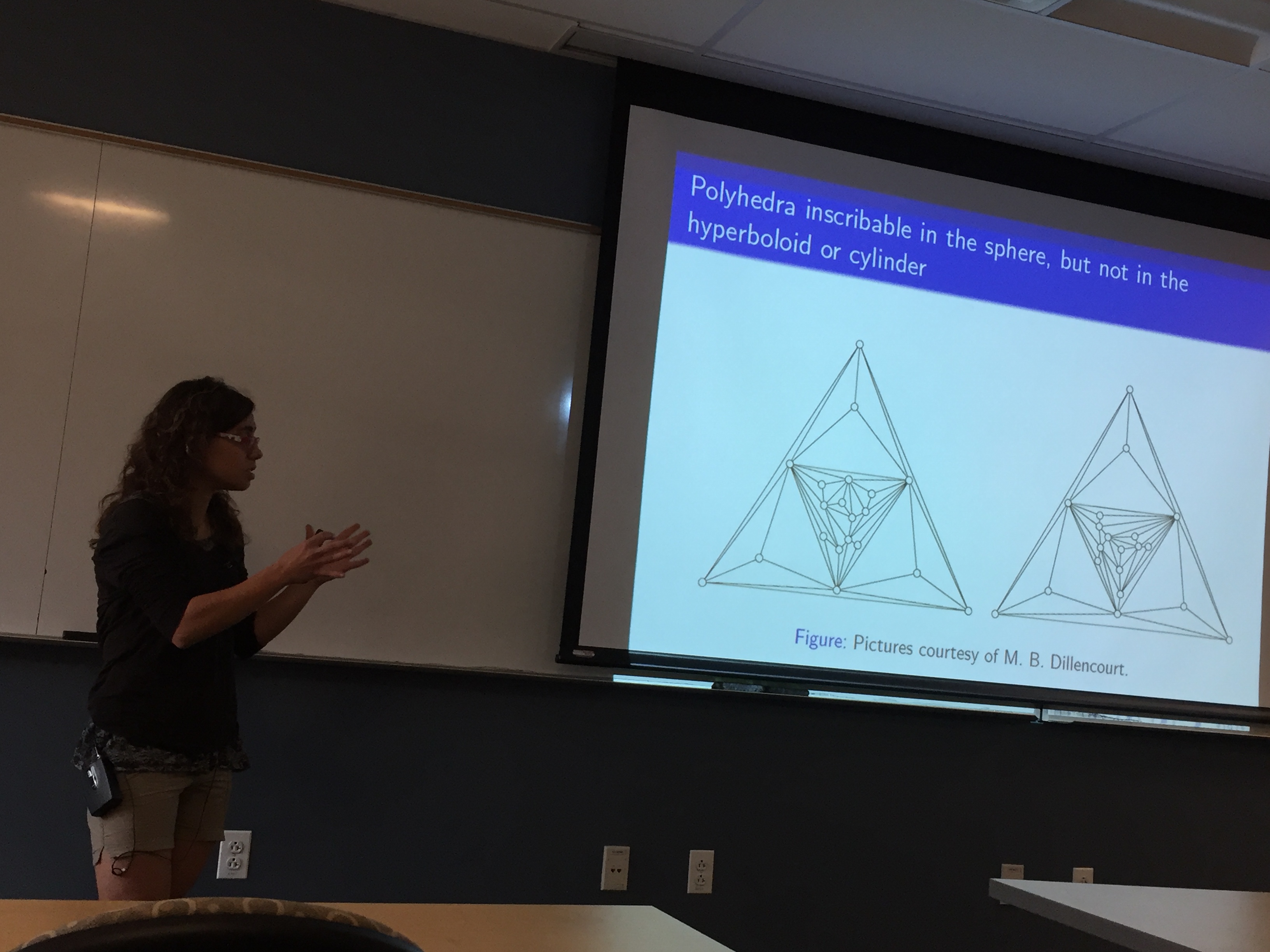
• October 21, 2016 Polyhedra inscribed in quadrics and their geometry
  Sara Maloni, University of Virginia
  

  

• October 14, 2016 Schottky groups and maximal representations
  Jean-Philippe Burelle, University of Maryland
  

  

• September 30, 2016 How to make 3-D printed sculptures of 4-D things. (Public Lecture)
  Henry Segerman, Oklahoma State University
  Special Location and Time: The HUB Ballroom, 2-3pm presention, 3-4pm book-signing.
  

  

• September 16, 2016 Introduction to hyperrings and hyperfields
  Jaiung Jun, Binghamton University
  

  

Spring 2016

• May 20, 2016 Positivity in Schubert Calculus, Part 2
  Rebecca Goldin, George Mason University
  

  

• May 13, 2016 Rank 1 Character Varieties
  Sean Lawton, George Mason University
  

  

• April 29, 2016 Positivity in Schubert Calculus
  Rebecca Goldin, George Mason University
  

  

• April 15, 2016 Geometry of the Vinberg’s Enveloping Monoid
  Chris Manon, George Mason University
  

  

• March 21, 2016 Voronoi Tilings and Loop Groups
  Pablo Solis , CalTech
  

  

• March 18, 2016 Algebraic Vision: the Quadrifocal Variety
  Luke Oeding, Auburn University
  

  

• March 4, 2016 The Gauss map and Diophantine approximation in the Heisenberg group
  Anton Lukyanenko, University of Michigan
  

  

• February 19, 2016 Genus of complete intersections in spherical varieties
  Kiumars Kaveh, University of Pittsburgh
  

  

• February 5, 2016 Strange duality of non-abelian theta functions
  Swarnava Mukhopadhyay, University of Maryland, College Park
  

  

Fall 2015

• December 18, 2015 Higgs bundles at the Fuchsian locus
  Richard Wentworth, University of Maryland, College Park
  

  

• December 4, 2015 Algebraic Properties of Skein Algebras of Surfaces
  Adam Sikora, State University of New York at Buffalo
  

  

• November 13, 2015 Stable Representation Theory and Spaces of Flat Connections
  Daniel Ramras, Indiana University-Purdue University Indianapolis
  

  

• November 6, 2015 A new approach to etale homotopy theory
  David Carchedi, GMU
  

  

• October 30, 2015 Geometry and Connectivity of Space of Finite Unit-Norm Tight Frames
  Nate Strawn, Georgetown
  

  

• October 9, 2015 Coordinates for representations of 3-manifold groups
  Christian Zickert, University of Maryland, College Park
  

  

• September 25, 2015 How to pinch a neck on a convex RP2 surface.
  John Loftin, Rutgers-Newark
  

  

Summer 2015

• July 24, 2015 Tropical computational experiments with compactifications of the deformation spaces of convex real projective structures on 2-orbifolds and surfaces
  Suhyoung Choi, Korean Advanced Institute of Science and Technology (KAIST)
  

Spring 2015

• April 24, 2015 The space of local overrings of an integral domain
  Neil Epstein, George Mason University

• April 10, 2015 Equations of tropical varieties
  Jeffrey Giansiracusa, Swansea University

  

• March 6, 2015 Proper affine deformations of the one-holed torus
  Todd Drumm, Howard University

  

• February 27, 2015 Zeta functions and motivic measures
  Niranjan Ramachandran, University of Maryland

  

• February 13, 2015 Complex dynamics and elliptic curves
  Laura DeMarco, Northwestern University

  

• January 30, 2015 Representation theory of symplectic singularities
  Ben Webster, University of Virginia
  

Fall 2014

• December 3, 2014 Primitive Geodesic Lengths and Arithmetic Progressions
  Ben McReynolds, Purdue University
  Special Time: 5-6pm

• November 19, 2014 Tameness of Margulis Spacetimes
  William Goldman, University of Maryland

• November 12, 2014 Homotopy of Character Varieties
  Sean Lawton, George Mason University

• October 29, 2014 The geometry of Euclidean polygons
  Chris Manon, George Mason University

• October 15, 2014 Counting Points on a Moduli Space
  Sean Lawton, George Mason University

 

For other talks/presentations, check our departmental Colloquium and Seminars.