Department of Mathematical Sciences
REU: Research experience for undergraduates

Multidisciplinary REU Program: Research, Education and Training in Computational Mathematics and Nonlinear Dynamics of Biological, Bio-inspired and Engineering Systems

The Department of Mathematical Sciences at GMU will host a multidisciplinary undergraduate research program in computational mathematics and nonlinear dynamics of biological, bio-inspired and engineering systems, from June 3 to Aug 2, 2013. The overall goal of this program is to encourage students and teachers to learn by discovery and enhance their understanding of the multidisciplinary role of mathematics in engineering, science, medicine and education.

Objective

This nine-week summer program will expose 12 highly qualified undergraduate students and 2 K-12 teachers to advanced topics in mathematics, mathematics education, problem-solving, visualization techniques and applications to bio-inspired and engineering systems. Through this program, we will not only provide the participants with a real-world experience of how mathematics can be applied to qualitatively and quantitatively study biological and engineering systems, but will also make it our priority to encourage women and under-represented minorities to pursue multidisciplinary careers that bridge the biological, mathematical, and computational sciences. This program will also help to train two K-12 teachers who will be able to use their problem-solving skills and research experience from the program to do open-ended exploration and develop related lesson studies in their high-school mathematics classrooms. In addition, three graduate students will be involved in this program as graduate mentors for the participants. The program will help nurture the intellectual growth and development of graduate students and also provide them with a valuable experience of mentoring.

Focus Areas

The three subprograms under the broad theme of computational mathematics and nonlinear dynamics that will help understand the quantitative behavior of biological, bio-inspired and engineering systems include:

• Modeling and analysis of biological, bio-inspired problems
  
  The students in this subprogram will be mentored to develop a thorough understanding of modeling, analysis and simulation of the problem within the context of the originating scientific discipline. They will be encouraged to suggest and explore possible modifications and then be shown how to systematically investigate the resulting processes. They will either write their own computational routines or be given access to more sophisticated numerical tools, as appropriate. Proposed research projects include:
  
  1. Computational modeling of Micro-Air Vehicles.
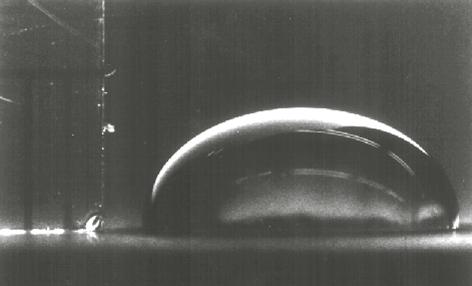
  2. Free-boundary Problems in Fluid Mechanics: Liquid Droplets on Surfaces.
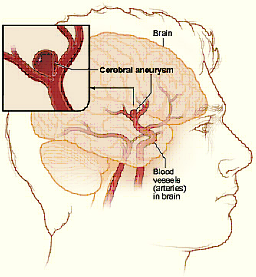
  3. Nonlinear Computational Biomechanics of Aneurysms.
  4. Bioinformatics applications.
  
  
• Mathematics of Materials
  
  In this REU subprogram, we will focus on reviewing existing mathematical optimization and modeling techniques that have helped materials scientists and engineers in obtaining more accurate results while utilizing efficient analytical and computational techniques. The students will be exposed to real world problems arising in interdisciplinary collaborations and will be trained in assessing complex problems and utilizing mathematical skills to build new and improve upon existing solutions - skills that are in great demand on both academic and industrial job market today. Possible projects include:
  
  1. Materials microstructure models.
  2. Free-boundary Problems in Fluid Mechanics: Liquid Droplets on Surfaces.
  3. Design of photovoltaic nanodevices.
  4. Phase diagram calculation.
  
  
• Mathematics Education
  
  The participants in this subprogram will learn about current software to create interactive computer-based demonstrations, issues of interfaces and controls, and how to evaluate effectiveness. Studying the research work related to student conceptual issues in the curriculum will influence the design intent. Students will propose problems or choose among suggested projects which they will pursue. Proposed research projects include: 1. Probability, Statistics and Engineering applications.
  2. Linear Systems, Precalculus and Calculus.
  3. Numerical Underpinning of Calculators and Computers.
  
  

Participant Support and Available Resources

All students will be selected on a competitive basis to participate in the program. Each selected student will receive a stipend of $3,375 and up to $550 travel allowance in addition to free housing and dining in the University residence hall for the duration of the program.

The Department of Mathematical Sciences will provide lab and office space. Participants will additionally be provided with unlimited access to campus computing, library, and recreational facilities and reduced admission fees to many campus events. Computational resources on campus include a large Beowulf-class parallel computing cluster with 134 CPUs (67 dual-processor Pentium III 600 Mhz nodes) running the Linux operating system. Each node is a Dell Precision410 Workstation with 512MB of RAM and 13GB of disk storage. Students will have access to several other Linux computer labs on campus 24 hours a day to support their research.

Application process

To apply, please submit the following materials by March 1, 2013:

1. Application form
2. Statement of purpose
3. Reference Form
   (Two to three reference letters must be received)
4. An official college transcript as of Spring 2013

You can submit these materials via email to reu AT math.gmu.edu, via fax to (703) 993-1491 or hard copies via regular mail to:

ATTN: REU Program Coordinators
Department of Mathematical Sciences
MS 3F2
George Mason University
4400 University Dr, Fairfax VA 22030.

Participating faculty

Dr. Padmanabhan Seshayier (PI)
Dr. Padmanabhan Seshaiyer is specially trained in numerical analysis, finite element methods, computational mechanics and scientific computing. Over the last few years, he has done extensive work on the theoretical and computational aspects of non-conforming hp finite element methods which will be used extensively for the computational modeling aspects of this research program. Dr. Seshaiyer's research in computational mathematics is highly multidisciplinary and has been funded by the NSF, the Whitaker foundation and the Texas ARP.

Dr. Maria Emelianenko (co-PI)
Dr. Maria Emelianenko's research is in the area of applied mathematics with main focus on the analysis and development of efficient numerical algorithms. Her research interests include working on problems arising on the interface between mathematical and physical sciences/engineering. Dr. Emelianenko has extensive experience supervising undergraduate research and has been playing an active role in various Women in Science and Engineering organizations.

Dr. Daniel Anderson
Dr. Daniel Anderson's research interests involve mathematical modeling and computational techniques applied to problems arising in fluid mechanics and materials science. He has been advising undergraduate research projects for the past several years and is one of the co-PIs on the NSF-sponsored CSUMS program in the Mathematical Sciences at GMU.

Dr. Harbir Lamba
Dr. Harbir Lamba's research areas include dynamical systems, numerical analysis and stochastic differential equations. Practical application areas of his research have included electrical engineering, mechanical engineering, and the modeling of financial markets.

Dr. Igor Griva
Dr. Igor Griva has an expertise in development of nonlinear optimization theory and methods. One of the possible applications of these algorithms is development of methodology for finding optimal design of nanosystems for efficient light manipulation (e.g. harvesting, transmission or localization). He has extensive experience supervising REU and other undergraduate research.

Dr. Jeng Lin
Dr. Jeng Lin is working in the area of nonlinear PDE analysis, focusing on stablity of Schrodinger equations. He coordinates the Summer Enrichment Program in Mathematics and Technology for Talented Youth at GMU.

Dr. Robert Sachs
Dr. Robert Sachs is researching the use of interactive demonstrations to enhance understanding and student inquiry in calculus, linear algebra and differential equations. He is currently mentoring a high school student on a related project. He is working on a calculus text, has spoken about calculus and shown demonstrations at meetings, and has been involved in several projects linking graduate students to pre-college education.