Daniel M. Anderson
Contents:
Imbibition of a Liquid Droplet on a Deformable Porous Substrate
We consider the imbibition of a liquid droplet into a deformable porous substrate. The liquid in the droplet is imbibed due to capillary suction in an initially dry and undeformed substrate. Deformation of the substrate occurs as the liquid fills the pore space. In our model, a pressure gradient in the liquid across the developing wet substrate region induces a stress gradient in the solid matrix which in turn leads to an evolving solid fraction and hence deformation. For axisymmetric droplets, we assume that the imbibition and substrate deformation at a given radial position are one-dimensional (in the vertical direction). The coupling to the droplet geometry leads to axisymmetric configurations for the deformed wet substrate. We show that the model chosen to describe the dynamics of the liquid droplet, based in this case on existing models developed for droplet spreading on rigid porous substrates, has little influence on the resultant swelling or shrinking of the substrate -- these general trends can be effectively predicted by a one-dimensional imbibition and deformation model -- but does strongly influence the details of the wet substrate shape. We characterize these predictions and in some cases can obtain analytical solutions for the evolution.
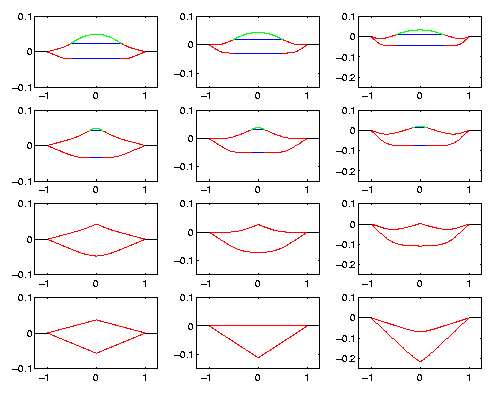
The following figure shows three time series of possible droplet imbibition scenarios corresponding to a fixed contact angle condition in the liquid droplet. In the first column eventual swelling occurs in the substrate. In the second column the substrate returns to an undeformed state. In the third column eventual shrinkage occurs in the substrate. The green boundary marks the top of the liquid droplet, the blue boundaries mark the wet substrate directly beneath the liquid droplet, and the red boundaries mark the deformed wet substrate region. The horizontal black lines at z=0 mark the undeformed surface of the porous substrate.
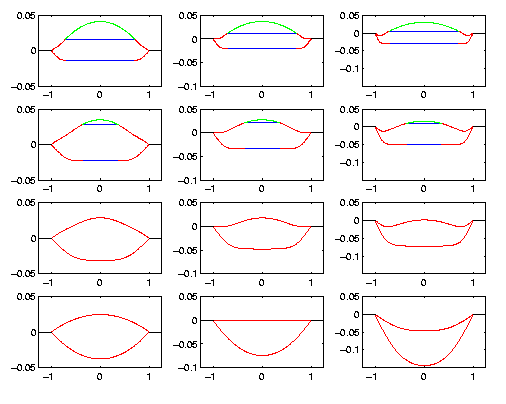
The following figure shows a similar time series as above but for a contact line condition in which the droplet maintains a constant curvature throughout the evolution.
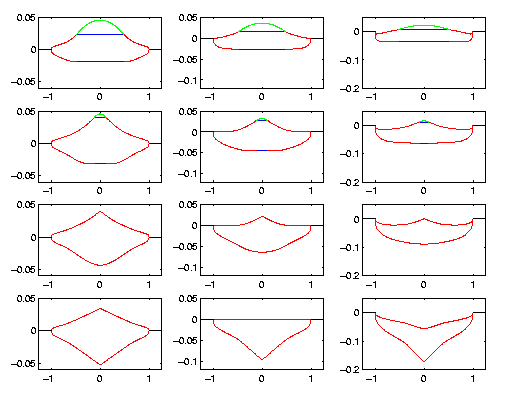
The following figure shows a similar time series as above but for a contact line condition in which the speed of the contact line is related to the contact angle.
An article on this work has been published in Phys. Fluids 17 (2005) 087104. PDF version of this article.
Capillary Rise of a Liquid into a Deformable Porous Material
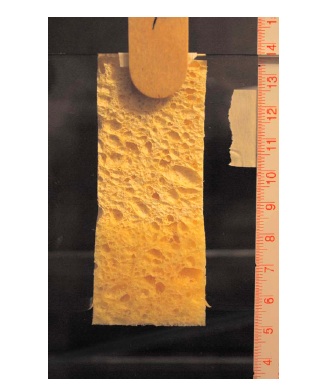
We examine the effects of capillarity and gravity in a model of one-dimensional imbibition of an incompressible liquid into a deformable porous material. We focus primarily on a capillary rise problem but also discuss a capillary/gravitational drainage configuration in which capillary and gravity forces act in the same direction. Models in both cases can be formulated as nonlinear free-boundary problems. In the capillary rise problem, we identify time-dependent solutions numerically and compare them in the long time limit to analytically obtain equilibrium or steady state solutions.Abasic feature of the capillary rise model is that, after an early time regime governed by zero gravity dynamics, the liquid rises to a finite, equilibrium height and the porous material deforms into an equilibrium configuration. We explore the details of these solutions and their dependence on system parameters such as the capillary pressure and the solid to liquid density ratio. We quantify both net, or global, deformation of the material and local deformation that may occur even in the case of zero net deformation. In the model for the draining problem, we identify numerical solutions that quantify the effects of gravity, capillarity, and solid to liquid density ratio on the time required for a finite volume of fluid to drain into the deformable porous material. In the Appendix, experiments on capillary rise of water into a deformable sponge are described and the measured capillary rise height and sponge deformation are compared with the theoretical predictions. For early times, the experimental data and theoretical predictions for these interface dynamics are in general agreement. On the other hand, the long time equilibrium predicted theoretically is not observed in our experimental data.
The figures below show the imbibition of water into a deformable sponge (left) and the measured overall wet-sponge height as a function of time. Two time regimes are observed: an early time in which the capillary rise and sponge deformation follow a square-root in time scaling a long time regime in which the dynamics follow a different power law.
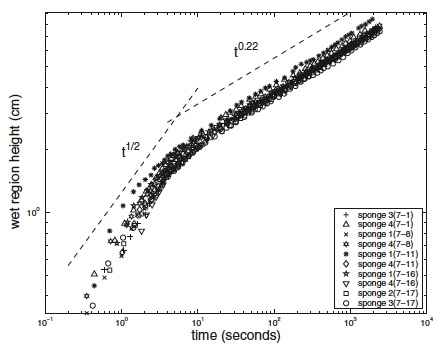
An article on this work has been published in Phys. Fluids 21 (2009) 013106. PDF version of this article.
Capillary Rise of a Liquid into a Deformable Porous Material
In this study we explore the one-dimensional capillary rise of a non–Newtonian, power-law fluid into rigid and deformable porous materials with and without gravity effects. For non–Newtonian flow in rigid porous materials with gravity, an equilibrium height equivalent to that for the classical Newtonian case is reached. However, the evolution toward the equilibrium solution differs between Newtonian and non-Newtonian cases. In the case of deformable porous material where both fluid and solid phases move, we use mixture theory to formulate the problem. Again equilibrium solutions exist and are the same for both Newtonian and non-Newtonian cases. In contrast to capillary rise in rigid porous material there are now two moving boundaries—the fluid height and the solid displacement at the bottom of the deforming porous material. In the absence of gravity effects, the model admits a similarity solution, which we compute numerically. With gravity present, the free boundary problem is solved numerically. In this case, the liquid rises to a finite height and the porous material deforms to a finite depth, following dynamics that depends on power-law index and power-law consistency index.
An article on this work has been published in J. Porous Media 14(12) (2011) 1087-1102.
Modeling wicking in deformable porous media using mixture theory
In this chapter we present a model for capillary wicking of a liquid into a deformable porous material. The model is derived using a mixture-theory approach in a general setting for solid and liquid constituents. We explore the predictions of the model for a one-dimensional capillary rise and deformation configuration. This problem involves two free boundaries -- an upper boundary associated with the capillary rise height of the fluid into the dry porous material and a lower boundary associated with the deforming solid interface in contact with a fluid bath. We outline results for both the zero gravity capillary rise/deformation case where similarity solutions can be obtained as well as the nonzero gravity capillary rise/deformation case where we identify time dependent and steady state solutions. Different permeability and solid stress models are investigated. We also present a comparison of the model predictions with experimental results available on capillary rise of water into deformable sponges.

Further details can be found in the book chapter by D.M. Anderson and J.I. Siddique entitled ``Modeling wicking in deformable porous media using mixture theory,'' in Wicking in Porous Materials: Traditional and Modern Modeling Approaches (eds. Reza Masoodi \& Krishna M. Pillai), (CRC Press), 2013. (ISBN: 978-1-4398-7432-5)
To Daniel M. Anderson's Homepage