Daniel M. Anderson
Contents:
The Averaging of Gravity Currents in Porous Media
We explore the problem of a slumping gravity current in the presence of a variable coefficient porous medium. We identify similarity variables and solutions for the uniform permeability case, and, using methods of homogenized averaging generalized to this nonlinear problem involving a moving boundary condition, make a connection to these similarity scalings in the case of variable coefficient layered media. We utilize these similarity scalings to identify half-height slumping time scales as a rough guide for field groundwater cleanup strategies involving injected salt water. By simplifying to a thin gravity current, retaining variations of the porous media in the horizontal direction, we derive a variable coefficient scalar nonlinear partial differential equation governing the moving interfaces. Through a combination of explicit homogenization retaining leading-order plus first-order corrections, and comparison with the full simulation of this simplified one-dimensional problem, we document the success of the homogenization approach for this nonlinear problem. In the context of a thin gravity current we also numerically address a case where the background permeability variation is in the vertical direction. The corrections identified exhibit a spatial imprint of the properties of the porous medium. Lastly, we provide a leading-order homogenization solution for a general case where permeability varies in both the horizontal and vertical dimensions, which results in coefficients that are accessible through the solution of a cell problem.
An article on this work has appeared in Phys. Fluids 15 (2003) 2810-2829. PDF version of this article.
On Gravity Currents in Heterogeneous Porous Media
We examine the case of density-dependent flow in heterogeneous porous medium systems bounded by a free surface using homogenization methods for leading-order approximations. Specifically we consider the two-dimensional case in which variations occur in both the horizontal and vertical directions. Such problems lead to the need to solve cell problems to compute the solution, which is generally done using numerical approaches. We review the general homogenization results for general topology and aspect ratio. We derive an analytical solution for a case with two-dimensional variability in the slender limit for certain assumed scaling of the permeability, and we find excellent agreement with the numerical solution. We also consider the case of two miscible fluids with an assumed sharp interface and contrasting densities. We derive an analytical solution in a thin limit neglecting mixing and show agreement with known solutions for limiting cases.
The first figure below shows a numerically calculated solution for a slumping gravity current with the background permeability as indicated, and a homogenized solution that makes use of an effective permeability computed with asymptotic averaging techniques. The homogenized solution captures the global dynamics of the gravity current while the full solution captures also the local signature of the permeability (see close up in second figure). Darker regions correspond to lower permeability values while lighter regions correspond to higher permeability values. The horizontal and vertical coordinates in the figures are in those for a slender geometry. This separation of scales indicates that the actual permeability structure has variation in the vertical direction that is much more rapid than that in the horizontal direction.
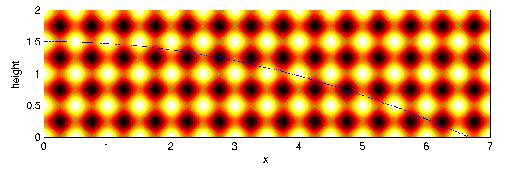
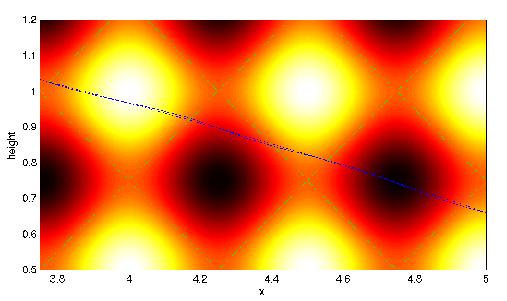
An article on this work entitled ``On Gravity Currents in Heterogeneous Porous Media,'' has been published in the Proceedings of the 15th International Conference on Computational Methods in Water Resources (CMWR XV), June 13--17 2004, Chapel Hill, North Carolina, Computational Methods in Water Resources, Volume 1, Developments in Water Science 55, eds. C.T. Miller, M.W. Farthing, W.G. Gray, and G.F. Pinder, pp. 303--312, (Elsevier Science, Amsterdam, The Netherlands, 2004). PDF version of this article.
A Sharp-Interface Interpretation of a Continuous Density Model for Homogenization of Gravity-Driven Flow in Porous Media
We examine homogenization methods applied to sharp-interface and diffuse-interface models for gravity-driven flow in heterogeneous porous media. Our work specifically examines a matrix of models that includes (1) a variable media, diffuse-interface model, (2) a variable media, sharp-interface model, (3) a homogenized media, diffuse-interface model and (4) a homogenized media, sharp-interface model. We connect all four of these models via homogenization theory and sharp-interface limits. We show that existing results based on homogenization methods applied to sharp-interface models can be recovered by a less direct but more rigorous approach involving well-established homogenization theory and sharp-interface limits.
An article on this work has appeared in Physica D. 239 (2010) 1855-1866. doi:10.1016/j.physd.2010.06.009 PDF version of this article.