Daniel M. Anderson
Polymer Drop Spreading
We develop a model to describe the dynamics of a spreading and melting droplet on a heated substrate. The model, developed in the capillary-dominated limit, is geometrical in nature and couples the contact line, tri-junction and phase-change dynamics. In this model the competition between spreading and melting is characterized by a single parameter that represents a ratio of time scales, one based on the thermal diffusivity and hot plate temperature and the other based on the characteristic contact line velocity. To highlight this competition, we compare the dynamics of the spreading and melting droplet to that of an isothermally spreading liquid drop whose dynamics are controlled exclusively by the contact line. Our modeling has been motivated by experiments performed by Glick in which polystyrene spheres show different spreading characteristics when subject to these two different thermal configurations. In addition to the competition between spreading and melting, we are also able to obtain information on the dynamics of the tri-junction. In our model, the equation of motion for the solid portion of the droplet acts in a natural way as a tri-junction condition. In contrast to models of tri-junction dynamics during solidification, where it is common to specify a tri-junction condition based on local physics alone, the tri-junction condition here must also account for global effects through a balance of forces over the entire solid--liquid interface.
The following set of plots shows the evolution of a solid droplet melting and spreading on a heated solid substrate. This evolution is representative of the case where the characteristic contact line speed is smaller than the characteristic thermal velocity
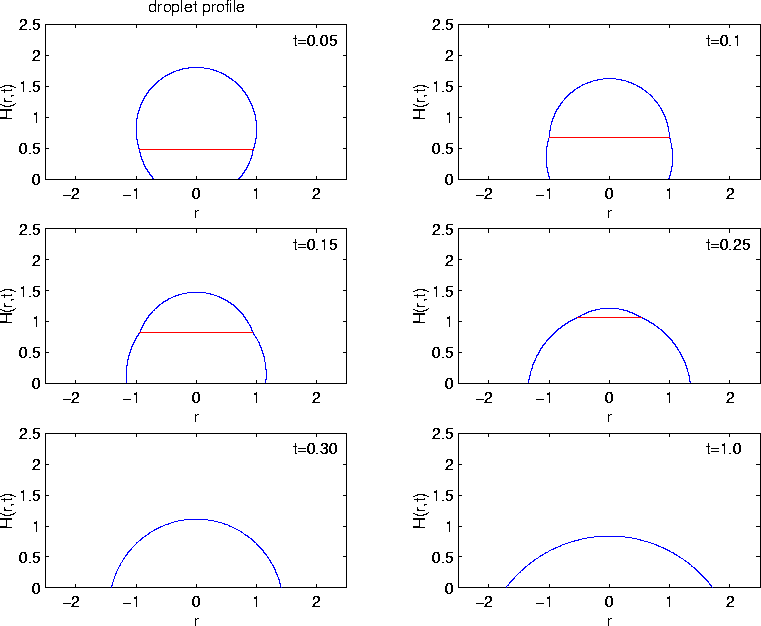
The following set of plots shows the evolution of a solid droplet melting and spreading on a heated solid substrate. Here the evolution is representative of the case where the characteristic contact line speed is larger than the characteristic thermal velocity
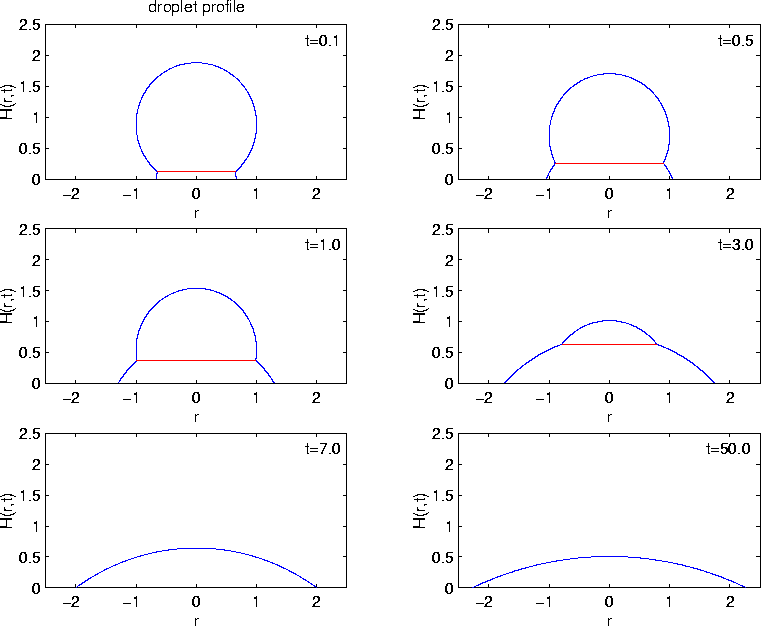
A paper on this topic can be found in SIAM J. Appl. Math 61 (2001) pp. 1502--1525. PDF version of this manuscript
To Daniel M. Anderson's Homepage