Daniel M. Anderson
Contents:
Weakly-Nonlinear Analysis of Mushy-Layer Solidification
We consider the solidification of a binary alloy in a mushy layer and analyse the system near the onset of buoyancy-driven convection in the layer. We employ a near-eutectic approximation and consider the limit of large far-field temperature. These asymptotic limits allow us to examine the rich dynamics of the mushy layer in the form of small deviations from the classical case of convection in a horizontal porous layer of uniform permeability. Of particular interest are the effects of the asymmetries in the basic state and the non-uniform permeability in the mushy layer, which lead to transcritically bifurcating convection with hexagonal planform. We obtain a set of three coupled amplitude equations describing the evolution of small-amplitude convecting states in the mushy layer. These equations are analysed to determine the stability of and competition between two-dimensional roll and hexagonal convection patterns. We find that either rolls or hexagons can be stable. Furthermore, hexagons with either upflow or downflow at the centres can be stable, depending on the relative strengths of different physical mechanisms. We determine how to adjust the control parameters to minimize the degree of subcriticality of the bifurcation and hence render the system globally more stable. Finally, the amplitude equations reveal the presence of a new oscillatory instability.
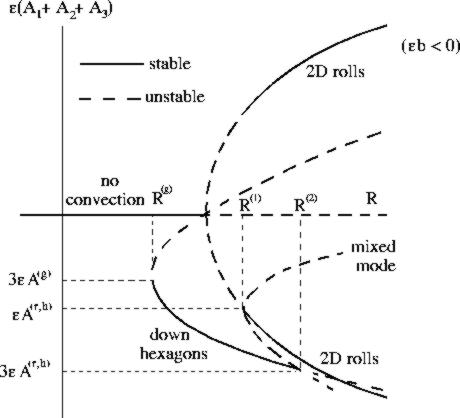
The following bifurcation diagram shows the stability of the nonconvecting state and of two-dimensional roll and three-dimensional hexagonal convecting states. The vertical axis represents the amplitude of convection and the horizontal axis represents the Rayleigh number. Depending on the parameter epsilon * b, hexagons with upflow at the center (up hexagons) or downflow at the center (down hexagons) can be stable. The mixed mode connecting rolls and hexagons is always unstable.
An article on this work has been published in J. Fluid Mech. 302 (1995) 307-331. PDF version of this article.
Oscillatory Instabilities in Mushy-Layer Solidification
We consider the solidification of a binary alloy in a mushy layer and analyse the linear stability of a quiescent state with specific interest in identifying an oscillatory convective instability. We employ a near-eutectic approximation and consider the limit of large far-field temperature. These asymptotic limits allow us to examine the dynamics of the mushy layer in the form of small deviations from the classical case of convection in a horizontal porous layer of uniform permeability. We consider also the limit of large Stefan number, which incorporates a key balance necessary for the existence of the oscillatory instability. The model we consider here contains no double-diffusive effects and no region in which a statically stable density gradient exists. The mechanism underlying the oscillatory instability we discover is instead associated with a complex interaction between heat transfer, convection and solidification.
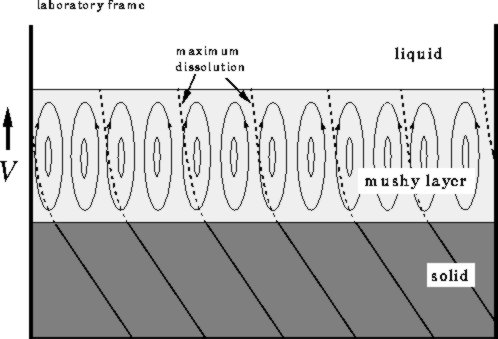
The following figure shows one possible scenario for neutrally stable (2D) travelling wave solutions. At any instant in time, the convection rolls and thermal fields are, to leading order, vertically oriented. However, as a result of a complex interaction between the solid fraction, thermal and flow fields in the mushy layer, the entire pattern translates horizontally as the mushy layer advances.
An article on this work has been published in J. Fluid Mech. 307 (1996) 245-267. PDF version of this article.
A Model for Diffusion-Controlled Solidification of Ternary Alloys in Mushy Layers
We describe a model for non-convecting, diffusion-controlled solidification of a ternary (three component) alloy cooled from below at a planar boundary. The modeling extends previous theory for binary alloy solidification by including a conservation equation for the additional solute component and coupling the conservation equations for heat and species to equilibrium relations from the ternary phase diagram. We focus on growth conditions under which the solidification path (liquid line of descent) through the ternary phase diagram gives rise to two distinct mushy layers. A primary mushy layer, which corresponds to solidification along a liquidus surface in the ternary phase diagram, forms above a secondary (or cotectic) mushy layer, which corresponds to solidification along a cotectic line in the ternary phase diagram. These two mushy layers are bounded above by a liquid layer and below by a eutectic solid layer. We obtain a one-dimensional similarity solution and investigate numerically the role of the control parameters on the growth characteristics. In the special case of zero solute diffusion and zero latent heat an analytical solution can be obtained. We compare our predictions with previous experimental results and with theoretical results from a related model based on global conservation laws described in the appendix. Finally, we discuss the potentially rich convective behavior anticipated for other growth conditions.
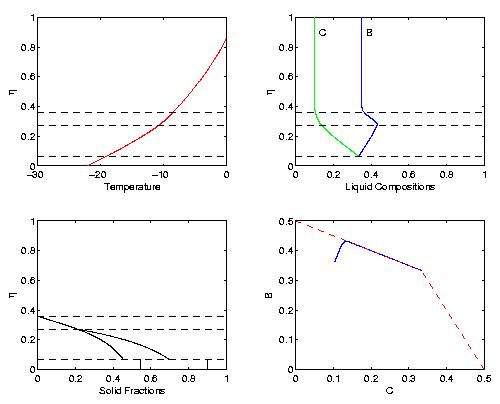
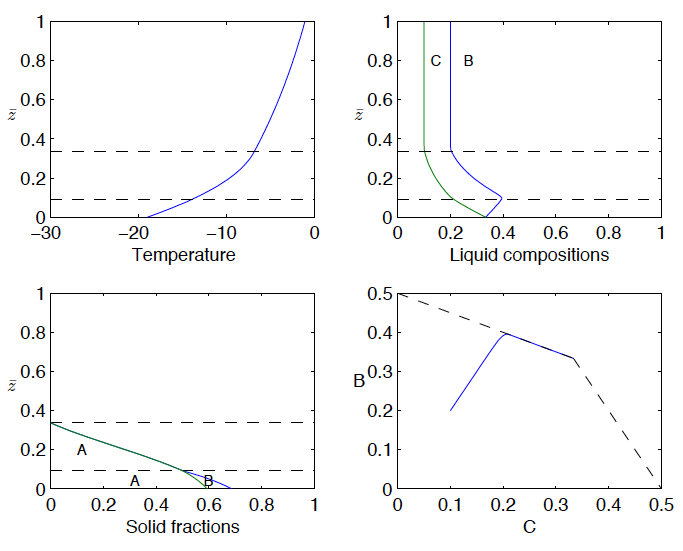
The following figure shows solutions for the diffusion-controlled solidification of a ternary alloy (species B and C dissolved in species A). The figures showing temperature, liquid compositions B and C and solid fraction distribution are plotted with respect to a similarity variable eta for a representative set of parameter values. The horizontal dashed lines indicate the interface positions separating (from top to bottom) the liqiud layer, the primary mushy layer, the secondary mushy layer and the eutectic solid layer. The lower right figure shows the solidification path in terms of the liquid compositions B and C. Here the dashed lines represent the cotectic boundaries that intersect at the ternary eutectic point.
An article on this work has been published in J. Fluid Mech. 483 (2003) 165-197. PDF version of this article.
Linear and Nonlinear Convection in Solidifying Ternary Alloys
In this work we consider buoyancy-driven flow and directional solidification of a ternary alloy in two dimensions. A steady flow can be established by forcing liquid downward at an average rate through a temperature gradient that is fixed in the laboratory frame of reference and spans both the eutectic and liquidus temperature of the material being solidified. Our results include both a linear stability analysis and numerical solution of the governing equations for finite amplitude, steady states. The ternary system is characterized by two distinct mushy zones---a primary layer with dendrites composed of a single species and, beneath the primary layer, a secondary layer with a dendritic region composed of two species. The two layers have independent effective Rayleigh numbers, which allows for a variety of convection scenarios.
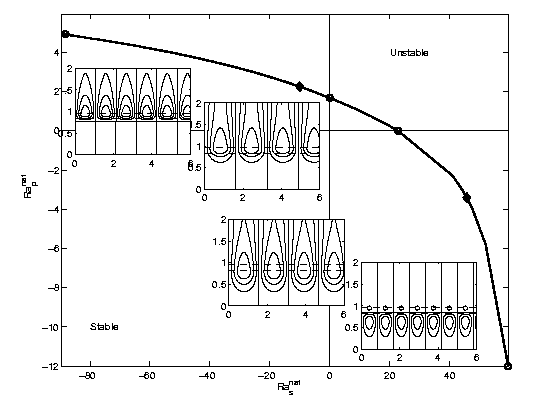
In this figure, the main solid line corresponds to the linear critical value of the Rayleigh numbers in the primary and secondary layers separating stable and unstable solutions. Inset plots show the buoyant convection patterns at the four circles along the main curve. Diamonds indicate the transition from single sets of rolls to stacked rolls.
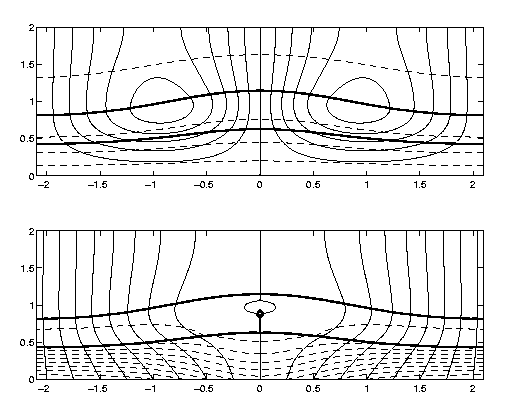
In the following figure, the upper plot shows streamlines associated with the buoyant convection (solid curves using equal spacing of 0.1 between contours) and isotherms (dashed curves using equal spacing of 0.25 between contours). The lower plot shows the streamlines for the total mass flux (solid curves) and the total solid fraction (dashed curves using equal spacing of 0.02 between contours). The diamond shows location of a liquid inclusion in primary mushy layer.
An article on this work has been published in J. Fluid Mech. 545 (2005) 213-243. PDF version of this article.
Convective Instabilities During the Solidification of an Ideal Ternary Alloy in a Mushy Layer
We consider a model for the solidification of an ideal ternary alloy in a mushy layer that incorporates the effects of thermal and solutal diffusion, convection and solidification. Our results reveal that although the temperature and solute fields are constrained to the liquidus surface of the phase diagram, the system still admits double-diffusive modes of instability. Additionally, modes of instability exist even in situations in which the thermal and solute fields are each individually stable from a static point of view. We identify these instabilities for a general model in which the base state solution and its linear stability are computed numerically. We then highlight these instabilities in a much simpler model that admits an analytical solution.
An article on this work has been published in J. Fluid Mech. 647 (2010) 309-333. PDF version of this article.
A three layer model for convection in a ternary alloy
This project examines the linear stability of a three layer (liquid, primary mush, secondary mush) ternary alloy system. This study extends previous ones decribed above to include the effects of solute diffusion and convection in a linear stability analysis. The base state solution is computed numerically, an example from Flynn's thesis is shown in the figure below. The linear stability of such base state solutions are examined using a Chebyshev pseudo-spectral method.
The figure below shows a typical base state solution with temperature, composition and solid fraction through the three layer ternary system.
This work is described in TJ Flynn's Master's Thesis, George Mason University, 2009.