Daniel M. Anderson
Contents:
A Diffuse-Interface Description of Fluid Systems
In classical models, an interface between two fluids is treated as infinitely thin, or sharp, and is endowed with properties such as surface tension. Diffuse-interface theories replace this sharp interface with continuous variations of an order parameter such as density in a way consistent with microscopic theories of the interface. Surface tension effects, for example, are incorporated into the model through a modified stress tensor in the classical Navier-Stokes equations. We relate the diffuse-interface model to classical, sharp interface models by deriving asymptotically the governing equations and the associated boundary conditions used in the sharp-interface formulation. We illustrate the diffuse-interface approach by modeling internal gravity waves, which have been observed experimentally by Berg et al. (Phys. Fluids 8 (1996) 1464) in xenon near its critical point. We obtain static density profiles, compute internal wave frequencies and compare with their experimental data and theoretical (classical) results both above and below the critical temperature. The results reveal a singularity in the diffuse-interface model in the limit of incompressible perturbations.
The full report on this work is published as NIST Internal Report 5887. PDF version of this manuscript.
A Diffuse-Interface Description of Internal Waves in a Near-Critical Fluid
We present a diffuse-interface treatment of the internal gravity waves which have been observed experimentally by Berg et al. in xenon near its thermodynamic critical point. The results are compared with theoretical predictions by Berg et al. (Phys. Fluids 8 (1996) 1464) that were obtained using separate models above and below the critical temperature. The diffuse-interface model applies both above and below the critical temperature, and is formulated by using the density as an order parameter. The diffuse interface is represented as a transition zone of rapid but smooth density variation in the model, and density gradients appear in a capillary tensor, or Korteweg stress term, in the momentum equation. We obtain static density profiles, compute internal wave frequencies and compare with the experimental data and theoretical results of Berg et al. both above and below the critical temperature. The results reveal a singularity in the diffuse-interface model in the limit of incompressible perturbations.
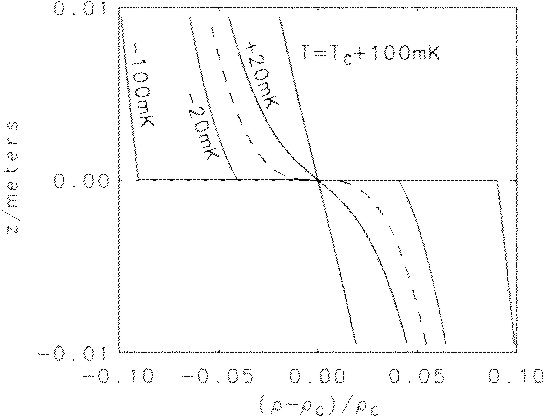
The figure below shows the static density profiles in a gravitational field as computed using a van der Waals equation of state to represent near-critical zenon. For temperatures above the critical temperature, there is stratification in a single-phase fluid. For temperatures below the critical temperature, a diffuse interface separates two stratified phases (the upper phase is vapor and the lower phase is liquid). The dashed line corresponds to the density profile at the critical temperature.
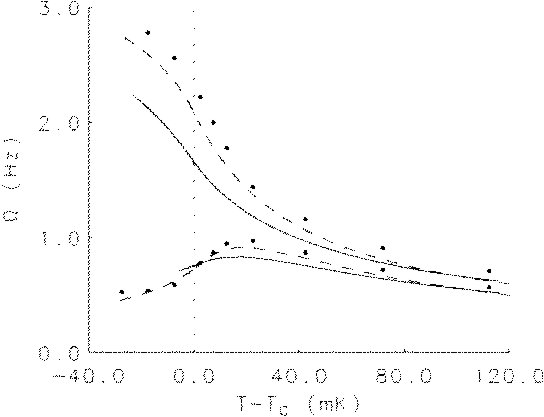
The figure below shows the internal wave frequencies (in Hz) obtained experimentally by Berg et al. (data points), the theoretical predictions by Berg et al. (dashed curves) using two separate models above and below the critical temperature coupled with a restricted cubic model for the equation of state, and the theoretical predictions of the diffuse-interface approach (solid curves) using a van der Waals equation of state. The diffuse-interface model applies both above and below the critical temperature. The vertical dashed line indicates the critical temperature.
A paper on this topic can be found in Phys. Fluids 9 (1997) 1870-1879. PDF version of this manuscript
A Diffuse-Interface Methods in Fluid Mechanics
We review the development of diffuse-interface models of hydrodynamics and their application to a wide variety of interfacial phenomena. These models have been applied successfully to situations in which the physical phenomena of interest have associated with them a length scale commensurate with the thickness of the interfacial region, (e.g.,~near-critical interfacial phenomena or small scale flows such as those occurring near contact lines), and fluid flows involving large interface deformations and/or topological changes (e.g.,~breakup and coalescence events associated with fluid jets, droplets, and large-deformation waves). We discuss the issues involved in formulating diffuse-interface models for single-component and binary fluids. Recent applications and computations using these models are discussed in each case. Further, we address issues including sharp-interface analyses that relate these models to the classical free-boundary problem, computational approaches to describe interfacial phenomena, and models of fully-miscible fluids.
A paper (also NIST Internal Report 6018) on this topic can be found in Ann. Rev. Fluid Mech. 30 (1998) 139-165. PDF version of this manuscript
A list of references to related work is also available.
A Phase-Field Model of Solidification with Convection
In this work we develop a phase-field model for the solidification of a pure material that includes convection in the liquid phase. The model permits the interface to have an anisotropic surface energy, and allows a quasi-incompressible thermodynamic description in which the densities in the solid and liquid phases may each be uniform. The solid phase is modeled by an extremely viscous liquid, and the formalism of irreversible thermodynamics is employed to derive the governing equations. We investigate the behavior of our model in two important simple situations corresponding to the solidification of a planar interface at constant velocity: density change flow and a shear flow. In the former case we obtain a non-equilibrium form of the Clausius-Clapeyron equation and investigate its behavior by both a direct numerical integration of the governing equations, and an asymptotic analysis corresponding to a small density difference between the two phases. In the case of a parallel shear flow we are able to obtain an exact solution which allows us to investigate the behavior of this flow in the sharp-interface limit, and for large values of the solid viscosity.
A paper (also NIST Internal Report 6237) on this topic can be found in Physica D 135 (2000) 175-194. PDF version of this manuscript
Thin Interface Asymptotics for an Energy/Entropy Approach to Phase-Field Models with Unequal Conductivities
Karma and Rappel recently developed a new sharp interface asymptotic analysis of the phase-field equations that is especially appropriate for modeling dendritic growth at low undercoolings [Phys. Rev. E 57 (1998) 4342]. Their approach relieves a stringent restriction on the interface thickness that applies in the conventional asymptotic analysis, and has the added advantage that interfacial kinetic effects can also be eliminated. However, their analysis focussed on the case of equal thermal conductivities in the solid and liquid phases; when applied to a standard phase-field model with unequal conductivities, anomalous terms arise in the limiting forms of the boundary conditions for the interfacial temperature that are not present in conventional sharp-interface solidification models, as discussed further by Almgren [SIAM J. Appl. Math. 59 (1999) 2086]. In this paper we apply their asymptotic methodology to a generalized phase-field model which is derived using a thermodynamically consistent approach that is based on independent entropy and internal energy gradient functionals that include double wells in both the entropy and internal energy densities. The additional degrees of freedom associated with the generalized phase-field equations can be chosen to eliminate the anomalous terms that arise for unequal conductivities.
A paper (also NIST Internal Report 6377) on this topic can be found in Physica D 144 (2000) 154-168. PDF version of this manuscript
A Phase-Field Model with Convection: Numerical Simulations
In a previously-developed phase-field model of solidification that includes convection in the melt [Anderson, McFadden and Wheeler, Physica D, 135 (2000) 175--194] the two phases are represented as viscous liquids, where the putative solid phase has a viscosity much larger than the liquid phase. In this paper we report numerical computations on a simplified form of this model which represents the growth of a two-dimensional dendrite in a thin gap between two parallel thermally insulting plates. In these computations flow in the liquid arises because of the differing densities of the solid and liquid phases.
A paper (also NIST Internal Report 6442) on this topic will be published in the proceeding of the conference `Interfaces for the Twenty-First Century' (eds. M.K. Smith, et al.) (2002). PDF version of this manuscript
A Phase-Field Model with Convection: Sharp-Interface Asymptotics
We have previously developed a phase-field model of solidification that includes convection in the melt [Anderson, McFadden and Wheeler, Physica D, 135 (2000) 175--194]. This model represents the two phases as viscous liquids, where the putative solid phase has a viscosity much larger than the liquid phase. The object of this paper is to examine in detail a simplified version of the governing equations for this phase-field model in the sharp-interface limit to derive the interfacial conditions of the associated free-boundary problem. The importance of this analysis is that it reveals the underlying physical mechanisms built into the phase-field model in the context of a free-boundary problem and, in turn, provides a further validation of the model. In equilibrium we recover the standard interfacial conditions including the Young-Laplace and Clausius--Clapeyron equations that relate the temperature to the pressures in the two bulk phases, the interface curvature and material parameters. In nonequilibrium we identify boundary conditions associated with classical hydrodynamics, such as the normal mass flux condition, the no-slip condition and stress balances. We also identify the heat flux balance condition which is modified to account for the flow, interface curvature and density difference between the bulk phases. The interface temperature satisfies a nonequilibrium version of the Clausius--Clapeyron relation which includes the effects of curvature, attachment kinetics and viscous dissipation.
A paper (also NIST Internal Report 6568) on this topic can be found in Physica D 151 (2001) 305-331. PDF version of this manuscript
A Phase-Field Model of Convection with Solidification
This paper describes numerical calculations for solidification in a Hele-Shaw cell when the effects of convection are present. The model is a ``two-fluid'' model in which the solid is modeled as a sufficiently viscous fluid. In particular, we investigate the effect of density change driven flow during dendrite solidification and also the effect of the viscosity ratio between the solid and liquid phases.
The figure below shows dendritic growth into an undercooled liquid for a solid to liquid density ratio of 1.1 (upper figure) corresponding to contraction during solidification and a density ratio of 0.9 (lower figure) corresponding to expansion during solidification.
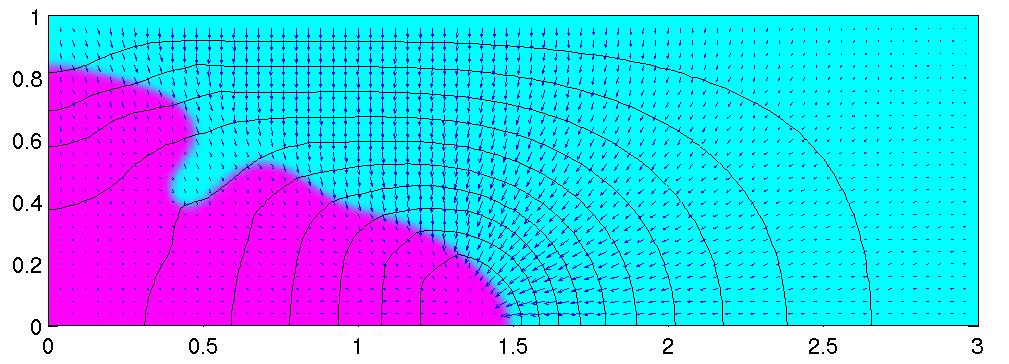
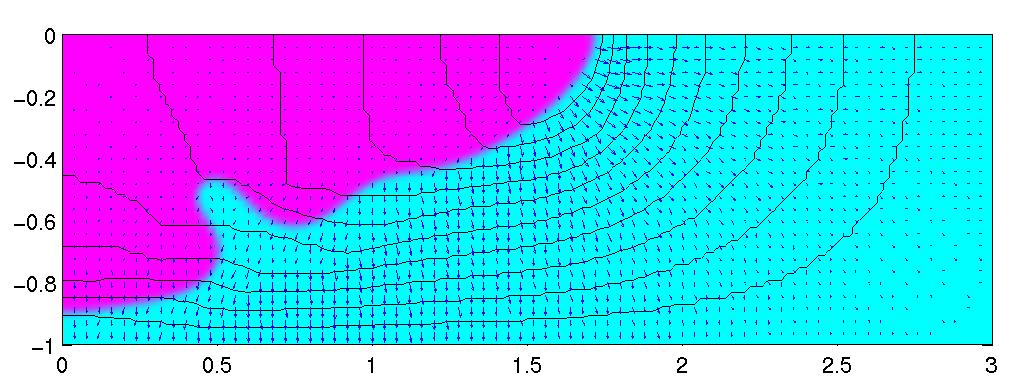
A paper on this topic can be found in AIAA 2002-0891 40th AIAA Aerospace Sciences Meeting and Exhibit (2002). PDF version of this manuscript
To Daniel M. Anderson's Homepage