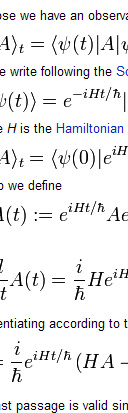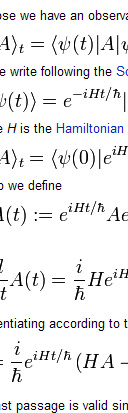My primary area of research is in the field of function theoretic operator theory. I study Multiplication, Composition and Weighted Composition operators on the Bloch space of bounded homogeneous domains in C^n. I try to connect the geometric and analytic properties of the symbols with the properties of the operator.
My dissertation is concerned with answering the following types of questions:
What types of symbols induce a bounded operator?
What is the norm of an operator, or what are bounds on the norm?
What types of symbols induce isometric or compact operators?
What is the spectrum of an operator?
What is the adjoint of an operator?
Publications:
Characterization of Isometries and Spectra of Multiplication Operators on the Bloch Space, Bulletin of the Australian Mathematical Society (to appear), with F. Colonna.
On the Isometric Composition Operators on the Bloch Space in C^n, submitted to the Journal of Mathematical Analysis and Applications, with F. Colonna.
Multiplication Operators on the Bloch Space of a Bounded Homogeneous Domain, in preparation, with F. Colonna.
Pattern Formation in Reaction-Diffusion Equations
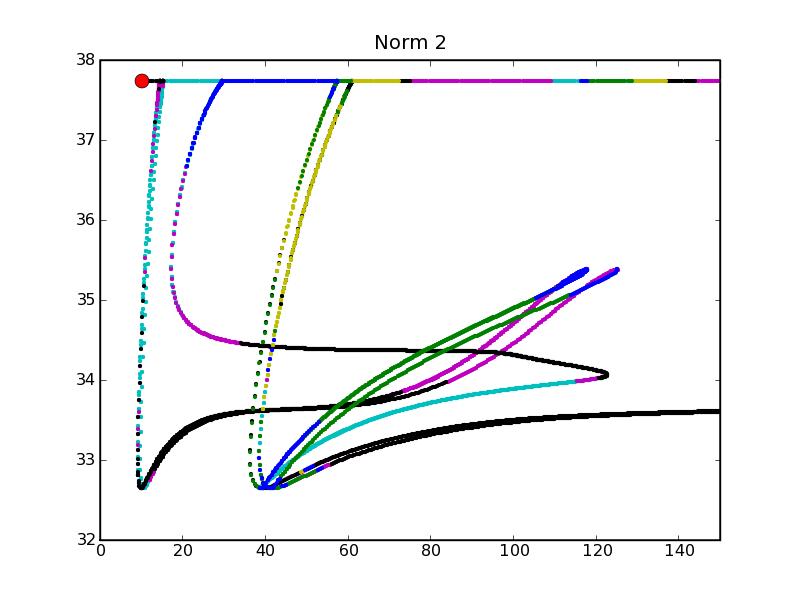
My secondary area of research falls in the intersection of Mathematical Biology and PDEs. I am interested in experimentally finding patterns exhibited by reaction-diffusion equations exhibiting Thomas instabilities. I use a pseudo-spectral method with AUTO to determine and construct bifurcation diagrams, as illustrated below.
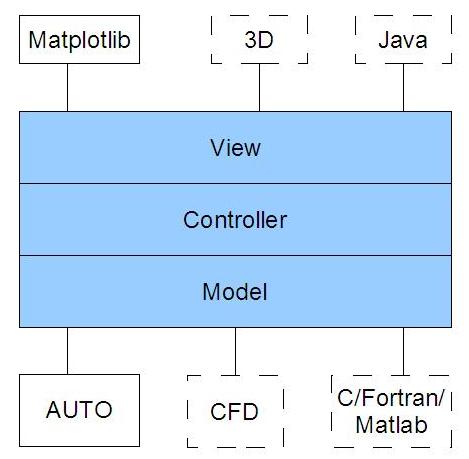
Out of this research stemmed the construction of a scalable visualization framework written in python. This framework allows for the visualization of one and two dimensional data, with three dimensional data to come soon. Currently, data from AUTO can be visualized by this framework. However, the design of the system was done in such a way that other scientific computing systems can be integrated. This line of research allows for me to utilize my undergraduate degree in computer science and my many years of experience as a software engineer.
Publications:
Stability Structures in Reaction-Diffusion Equations with Turing Instabilities, in preparation, with E. Sander and T. Wanner.
Scalable Visualization Framework for Scientific Computing, in preparation, with E. Sander and T. Wanner.