Class
Activity
(not for credit)
Groups of 3-4 students each
1. Consider the dihedral group D6 of symmetries of a hexagon.
a. Let H be the subgroup of rotations by 0, 120, or 240 degrees (notice that these are not all rotations).
b. State Lagrange's theorem. What does it imply about how many left cosets are there?
c. List the left cosets.
d. Is H normal in D6? Check by looking at the right cosets and comparing them to the left cosets. For H to be normal, you need aH=Ha for each element a in D6.
e. Suppose D6/H were a group under the operation (aH)(bH)=(ab)H. Try to construct a Cayley table for the product and show directly that the product is, or is not, well-defined. There are three ways to write the name of any of the 4 cosets. To show it's well-defined this way, you need to check that the product of two cosets is the same coset no matter which of the three names you use. You need to check all the products of all three ways of writing the same coset. To show it's not well-defined, you need only show that the product of some particular cosets is different depending on which element you use to represent the cosets.
f. Use a theorem about normal subgroups (and your anwer to whether H is normal in D6) to conclude whether D6/H is a group or not under the operation (aH)(bH)=(ab)H.
Activity for 12:30-12:50
Everyone switch groups. New groups of 2-3 people, none of whom were previously grouped together in the first round, if that's possible.
2. We used the orbit-stabilizer theorem in class to show that the cube has 24 rotational symmetries. Let G be the group of rotational symmetries.
a. First, convince yourself of this fact by letting G act on the set of vertices. Pick one vertex of the cube. What is the size of its orbit? What is the size of its stabilizer? What does the orbit-stabilizer theorem tell us?
b. Second, convince yourself another way: let G act on the set of faces of the cube. What is the size of its orbit? What is the size of its stabilizer? What does the orbit-stabilizer theorem tell us?
c. We showed that the rotational symmetries of the tetrahedron was isomorphic to A4. Are the rotational symmetries of a cube isomorphic to S4? If so, exhibit an explicit isomorphism. If not, explain why no isomorphism can exist.
Activity for 12:50-1:15
Stay in the same groups. Short answer:
3a. Are
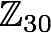
and
isomorphic? Prove your answer.
3b. Let G be cyclic, and suppose H is isomorphic to G. Is H necessarily cyclic? Prove it.
3c. Suppose that a group has size 17. What can you say about the group?