Harbir Antil - Research

Modeling, Simulation and Shape Optimization of Surface Acoustic Wave Driven Microfluidic Biochips

Fig 1: Microfludic biochip with microchannels

and two hexagonal reservoirs, typical characteristic

length is O(mm).

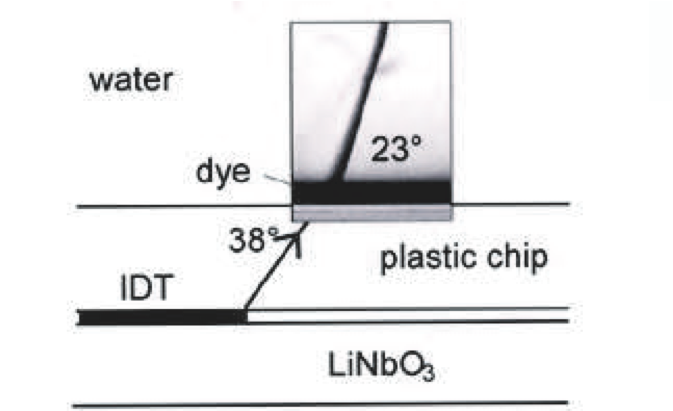Fig 2: A sharp jet is created by an interdigital transducer (IDT), placed on a piezoelectric substrate (lithium niobate in our case) and steers out surface acoustic waves (SAWs), which in turn makes the fluid to move (experimental setup).

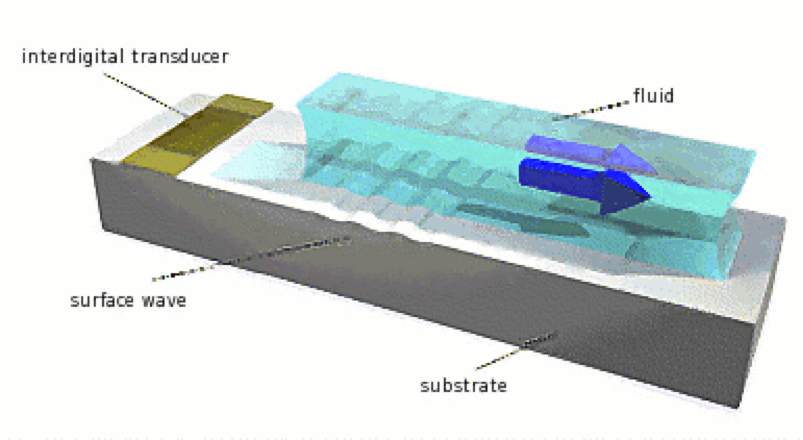Fig 3: A cartoon with further elaboration of the phenomenon explained in left figure (courtesy: D. Köster [2006]).

Modeling Equations

The state equations represent a multiscale multiphysics problem consisting of the linearized equations of piezoelectricity and compressible Navier-Stokes equations.
A standard homogenization approach is applied, which results in a first order time periodic linearized compressible Navier-Stokes equations with time scale [0,T₁], where T₁ is O(ms) (cf. Fig 5).
And a second order compressible Stokes system with time scale [0,T₂] which results in an almost stationary pattern called acoustic streaming. Here T₂ is O(µs) (cf. Fig 6).

Model Validation

Fig 4: Experimentally obtained acoustic streaming pattern.

In order to validate our model we consider a square domain (0,1)² mm². The video on the left (Fig 5) shows a SAW entering the domain and Figure 6 on the right shows the stationary surface acoustic streaming pattern formed. Figure 4 shows the experimentally obtained stationary surface acoustic streaming pattern. Qualitatively and quantitatively our numerical results matches quite well the experiments.

Surface Acoustic Wave

Fig 5: A SAW entering entering in the domain using an IDT placed at the bottom left corner.

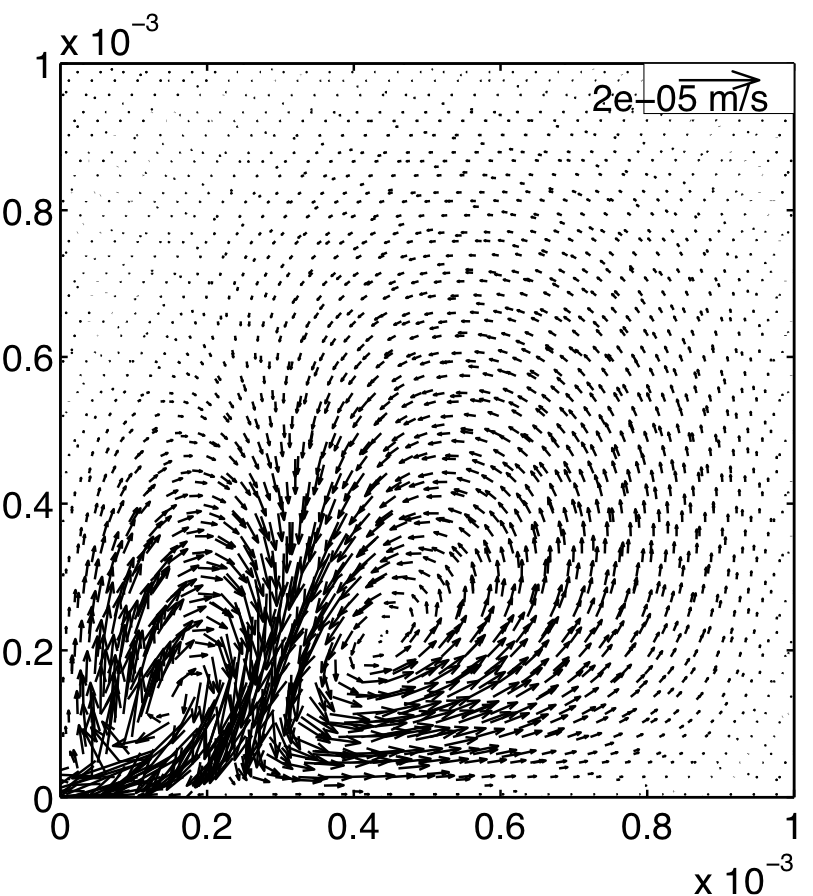Fig 6: Stationary acoustic streaming pattern.

Goal

After validation of our model using the experiments, the next goal of this project is to ensure that the hexagonal reservoirs in biochip are filled with precise amount of fluid and vorticity is minimized (cf. Fig 7). This requires us to do shape optimization of capillary barriers marked in red in Figure 8. Hence we need to solve a PDE constrained optimization problem subject to microfluidic biochip equations (see Modeling Equations above) as constraints.

Fig 7: Experimental filling of hexagonal shaped reservoirs which are part of microfluidic biochip.

Fig 8: In order to ensure that the reservoirs are filled with precise amount of fluid we want to do shape optimization of the capillary barriers (marked in red) and since remaining part of the domain is large and fixed there we apply model reduction. As a result we have to solve a system of very small size as compared to a huge problem during optimization.

Collaborators

Matthias Heinkenschloss (Rice University)
Ronald H. W. Hoppe (University of Houston)
Achim Wixforth (University of Augsburg)

Achievements

Since the nonlinearities due to shape variation is localized in small part of the domain, we use domain decomposition and apply model reduction to large part of the domain which is fixed and use full order model on the variable domain.
We have proven error estimated for the error between the solution of the original and the reduced order problem. The error estimate depend on the model reduction error estimate.
The computational results are validated by the actual experiments, and may further lead to better manufacturing of the microfludic devices.

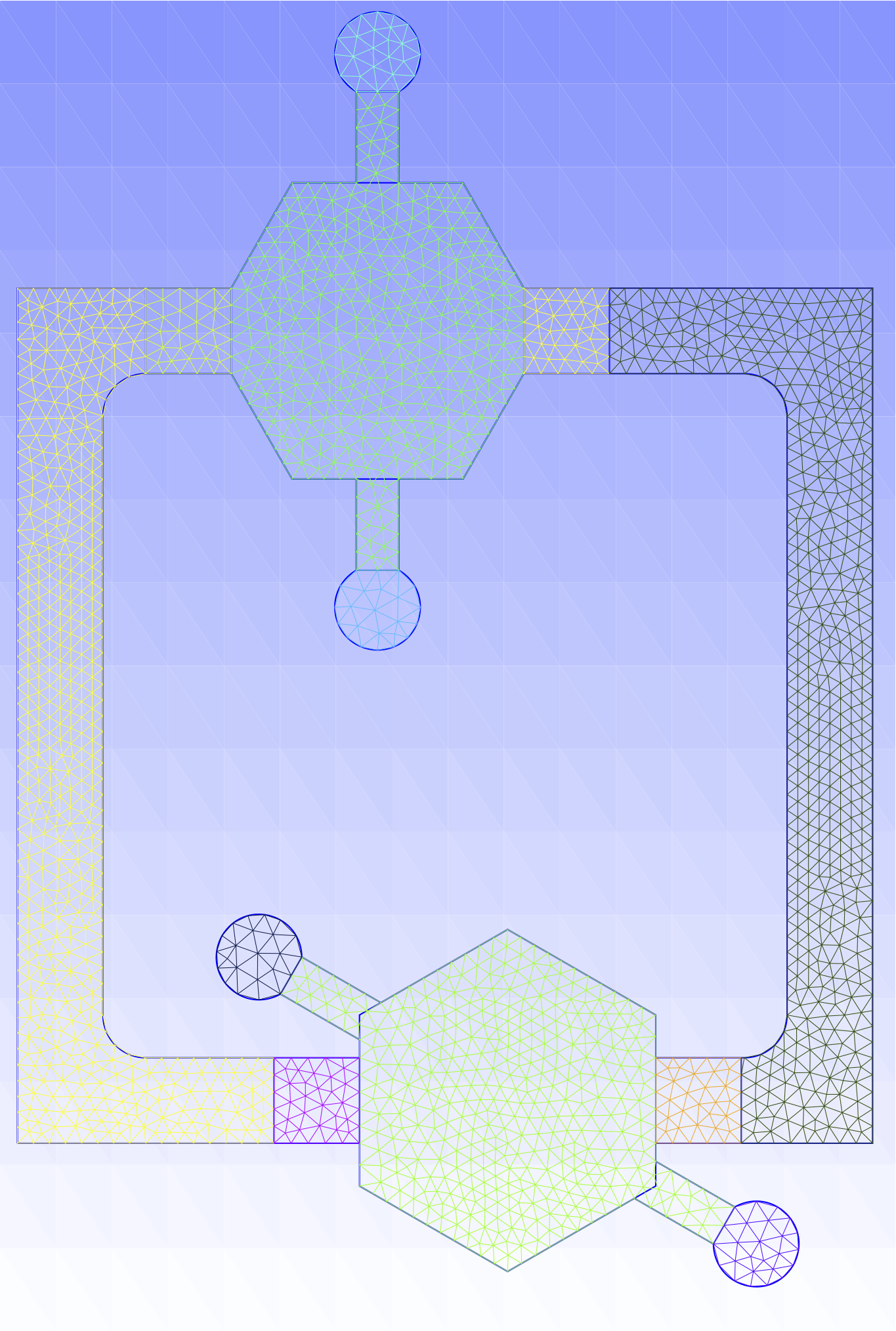Fig 9: A finite element mesh generated for the microfluidic biochip using gmsh.

Related Publications

H. Antil, R.H.W. Hoppe, C. Linsenmann, and A. Wixforth.
Reduced Order Modeling Based Shape Optimization of Surface Acoustic Wave Driven Microfluidic Biochips.
Mathematics and Computers in Simulation (2010). link

H. Antil, R. Glowinski, R.H.W. Hoppe, and C. Linsenmann, T.-W. Pan, and A. Wixforth.
Modeling, Simulation, and Optimization of Surface Acoustic Wave Driven Microfluidic Biochips .
Journal of Computational Mathematics (2010), 28(2):149--169. link